Question

For the given circuit, three resistances $R$ , $2R$ and $6R$ are given. Ratio of power developed across $R$ , $2R$ and $6R$ will be:

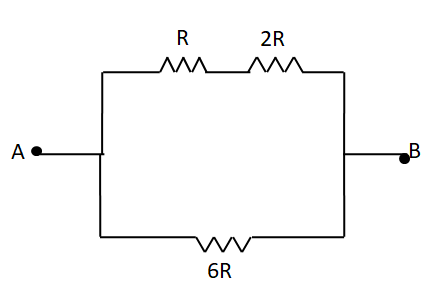
(A) $1:2:3$
(B) $2:4:3$
(C) $3:5:8$
(D) ${\text{4:3:5}}$

Answer 1

To solve this question, we need to imagine a voltage source supplying the power to the system. Then, using the current division rule to distribute the current among the resistors and using the formula of the power, we can get the required ratio.
The formula used to solve this question is
$\Rightarrow P = {I^2}R$
Where $P$ is power developed across a resistance of $R$ through which a current $I$ is flowing.

Complete step by step answer:
We know that the power developed across a resistance $R$ is given by
$\Rightarrow P = {I^2}R$ ……………... (i)
We have the values of all the resistances, but don’t have any value current flowing through them. So, first we have to find out the current flowing through each of the resistors. For that, we need to assume a DC power source which supplies power to the circuit given. This is as shown in the below circuit diagram.

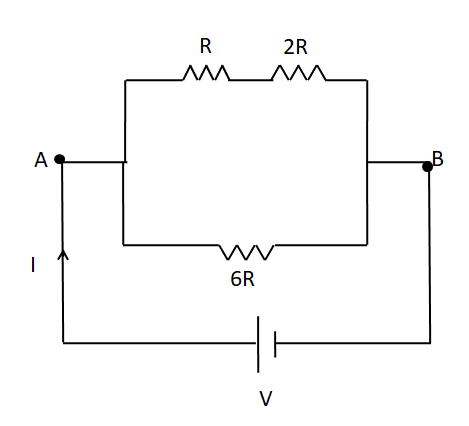
Let the battery supply a net current of $I$ . Now, we need to distribute this current in the two branches of this circuit. For that, we must know the resistance in each branch.
The resistance in the lower branch is clearly equal to $6R$ .
In the upper branch, we have $R$ and $2R$ arranged in series. We know that resistances in serial combination get added up. So, the equivalent resistance in the upper branch is equal to
$\Rightarrow {R_e} = R + 2R$
$\Rightarrow {R_e} = 3R$
So, we can redraw the upper circuit as

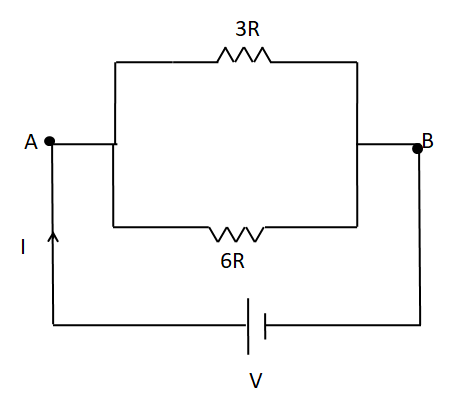
As can be seen in the above circuit diagram, the two resistances are arranged in parallel combination having the same potential difference across them. From Ohm’s law we know that
$\Rightarrow I = \dfrac{V}{R}$
So, for the same potential difference $V$ the current is inversely proportional to the resistance.
The resistances in the upper and the lower branches are in the ratio of
$\Rightarrow \dfrac{{3R}}{{6R}} = \dfrac{1}{2} = 1:2$
As the current is inversely proportional, so its ratio in the upper and the lower branches is the inverse of the ratio of the resistance, that is, $2:1$
So, according to the ratio we assume the currents in the upper and the lower branches as $2{I_1}$ and ${I_1}$ respectively, as shown below.

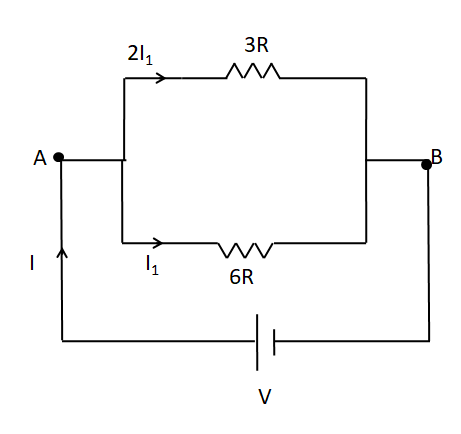
Now, we again separate the two resistances in the upper branch.

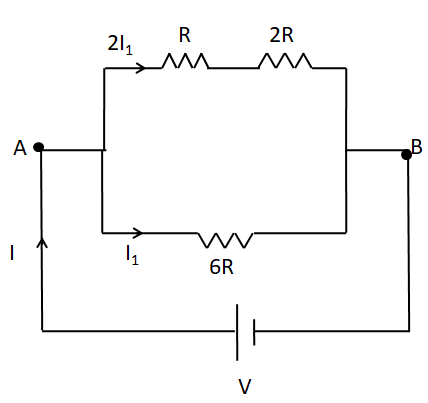
As the current in series is the same, so the current through both the resistances $R$ and $2R$ is equal to $2{I_1}$ .
Now, from the equation (i) we calculate the power developed across each resistance.
Now, power developed across $R$ is
$\Rightarrow {P_1} = {\left( {2{I_1}} \right)^2}R$
$\Rightarrow {P_1} = 4{I_1}^2R$ ……………... (ii)
Power developed across $2R$ is
$\Rightarrow {P_2} = {\left( {2{I_1}} \right)^2}\left( {2R} \right)$
$\Rightarrow {P_2} = 8{I_1}^2R$ ……………... (iii)
Power developed across $6R$ is
$\Rightarrow {P_2} = {\left( {{I_1}} \right)^2}\left( {6R} \right)$
$\Rightarrow {P_2} = 6{I_1}^2R$ ……………... (iv)
From (ii), (iii) and (iv), we have
$\Rightarrow {P_1}:{P_2}:{P_3} = 4:8:6 = 2:4:3$
Thus, the ratio of power developed across $R$ , $2R$ and $6R$ is $2:4:3$

Hence, the correct answer is option B.

Note: We can use the second formula of power also to solve the same question, which is given by $P = \dfrac{{{V^2}}}{R}$ . For using this, we have to use the voltage division rule to distribute the voltages across each resistance and calculate the required ratio of power developed across the resistances.