Question

For the given circuit, the potential ${V_M} - {V_N}$ between points $M$ and $N$ is equal to zero when

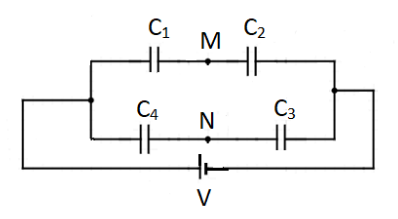
A. ${C_1}{C_4} = {C_2}{C_3}$
B. $\dfrac{{{C_1}}}{{{C_3}}} = \dfrac{{{C_1} + {C_2}}}{{{C_3} + {C_4}}}$
C. $\dfrac{{{C_2}}}{{{C_4}}} = \dfrac{{{C_1} + {C_2}}}{{{C_3} + {C_4}}}$
D. All of these

Answer 1

The potential differences across the four capacitors are calculated. The property that the charges of the capacitors that are connected in series are equal is applied and the formula relating the charge, potential difference and capacitance of a circuit is applied and corresponding equations are constructed. The equations for the potentials ${V_M}$ and ${V_N}$ are found out and subtracted from each other to obtain the equation in terms of the four capacitances of the circuit.

Complete step by step answer:
The potential across point M is denoted by ${V_M}$ and the potential across point N is denoted by ${V_N}$. We need to first determine the potential differences across each capacitor so that we can apply that in the general formula for capacitance in a circuit. This formula is as follows:
$C = \dfrac{q}{V}$
where, $q$ is the charge passing through or held by the capacitor, $V$ is the potential across the capacitor and $C$ is the capacitance which is the proportionality constant.
The capacitance is defined as the amount of charge required to increase the potential of the conductor by a unit amount. The terms can be rearranged to get:
$q = CV$ ---($1$)
Next, we need to calculate the potential difference for all the capacitors. This is done by subtracting the value of a lower potential value from a higher potential value. This will give the potential difference across a capacitor. From the above circuit we can see that, the potential difference across ${C_1}$ is: $V - {V_M}$

Since the voltage point ${V_M}$ is connected to the negative potential of the source voltage $V$ the potential is taken to be zero since the current in a conventional circuit flows from the positive to the negative potential and the electrons get collected at the negative end and this value of voltage is zero.
The potential difference across ${C_2}$ is: ${V_M} - 0 = {V_M}$
The potential difference across ${C_3}$ is: $V - {V_N}$
Since the voltage point ${V_N}$ is connected to the negative potential of the source voltage $V$ the potential is taken to be zero.
The potential difference across ${C_4}$ is: ${V_N} - 0 = {V_N}$
There is a property that if two capacitors are connected in series then their corresponding charges passing through them are equal.
Since capacitors ${C_1}$ and ${C_2}$ are in series connection:
${q_1} = {q_2}$
Applying the formula from equation ($1$)
${q_1} = {C_1}(V - {V_M})$
$\Rightarrow {q_2} = {C_2}{V_M}$

Since these two charges are equal we equate the above equations correspondingly:
${C_1}(V - {V_M}) = {C_2}{V_M}$
The terms in brackets are expanded and
$\Rightarrow {C_1}V - {C_1}{V_M} = {C_2}{V_M}$
We then rearrange the terms and manipulate to find the value of ${V_M}$ and hence make ${V_M}$ the subject.
$\Rightarrow {C_1}V = {C_1}{V_M} + {C_2}{V_M}$
Taking the value of ${V_M}$ out as common we get:
$\Rightarrow {C_1}V = {V_M}({C_1} + {C_2})$
$\Rightarrow {V_M} = \dfrac{{{C_1}V}}{{{C_1} + {C_2}}}$ ---($3$)
Next we must find the value for ${V_N}$
Since capacitors ${C_3}$ and ${C_4}$ are in series connection:
${q_3} = {q_4}$
Applying the formula from equation ($1$)
${q_3} = {C_3}(V - {V_N})$
$\Rightarrow {q_4} = {C_4}{V_N}$

Since these two charges are equal we equate the above equations correspondingly:
${C_3}(V - {V_N}) = {C_4}{V_N}$
The terms in brackets are expanded and
$\Rightarrow {C_3}V - {C_3}{V_N} = {C_4}{V_N}$
We then rearrange the terms and manipulate to find the value of ${V_M}$ and hence make ${V_M}$ the subject.
$\Rightarrow {C_3}V = {C_3}{V_N} + {C_4}{V_N}$
Taking the value of ${V_N}$ out as common we get:
$\Rightarrow {C_3}V = {V_N}({C_3} + {C_4})$
$\Rightarrow {V_N} = \dfrac{{{C_3}V}}{{{C_3} + {C_4}}}$ ---($4$)
The equations obtained in ($3$) and ($4$) are manipulated and the equation ($4$) is subtracted from equation ($3$). This gives:
${V_M} - {V_N} = \dfrac{{{C_1}V}}{{{C_1} + {C_2}}} - \dfrac{{{C_3}V}}{{{C_3} + {C_4}}}$

The potential difference between the points ${V_M}$ and ${V_N}$ is said to be zero which is given in our question.
$0 = \dfrac{{{C_1}V}}{{{C_1} + {C_2}}} - \dfrac{{{C_3}V}}{{{C_3} + {C_4}}}$
Taking out the common term $V$ outside and cancelling it out, we get:
$\Rightarrow \dfrac{{{C_1}}}{{{C_1} + {C_2}}} = \dfrac{{{C_3}}}{{{C_3} + {C_4}}}$
The terms are cross multiplied to get the final equation in terms of the four capacitances in the circuit.
$\therefore \dfrac{{{C_1}}}{{{C_3}}} = \dfrac{{{C_1} + {C_2}}}{{{C_3} + {C_4}}}$

Hence the correct option is B.

Additional information: The electrical capacitance of a conductor is the measure of its ability to hold electric charge. The role of a capacitor is to store charge by using the process of charging and discharging cycles. When an insulated conductor is given some charge then it acquires a certain potential and when there is an increase in charge it is observed that the potential also is increased and hence these two quantities are directly proportional. The constant $C$ denoting capacitance was hence introduced which signifies that it is the equivalent to the charge required to increase the potential of the conductor by a unit amount.

Note: There is a possibility of reducing the circuit into a single circuit by applying the capacitor in series and parallel formulae which in this case would be wrong. This method must be avoided as the aim here is to find an equation in terms of capacitance finding out the potential differences between the two points. Another mistake which can be made is when calculating the potential difference where the negative potential of the source voltage is connected to point ${V_M}$ and hence the voltage of this part of the source voltage is taken to be $0$ potential.