Question

For the given circuit find out the –

(a) total resistance of the circuit across the battery terminals.
(b) potential difference between A and B.

Answer 1

First, check whether the wheatstone bridge in the given circuit is balanced. Then use the formula for the effective resistance of two resistances in series and two resistances in parallel connection to find the total resistance of the circuit. Use Ohm’s law to calculate the current in the circuit.

Formula used:
When two resistances are in series connection, the equivalent resistance of the two is given as ${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$.
When two resistances are in parallel connection the equivalent resistance of the two are given as ${{R}_{eq}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$
$\Delta V=i{{R}_{eq}}$,
where i is the current passing through the battery and $\Delta V$ is the potential difference produced by the battery.

Complete step by step answer:
(a) In the given figure, we can see that the circuit consists of a Wheatstone bridge.

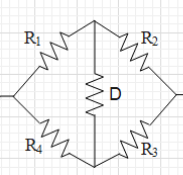
If the wheatstone bridge is balanced then the current in the bridge resistance (D) will be zero.
The condition for a wheatstone bridge to be balanced is that $\dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{R}_{3}}}{{{R}_{4}}}$.
In this case, ${{R}_{1}}={{R}_{2}}={{R}_{3}}={{R}_{4}}=2\Omega$.
Then this means that $\dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{2}{2}=\dfrac{{{R}_{3}}}{{{R}_{4}}}=1$.
Therefore, the wheatstone bridge is balanced. This means that is no current flowing in the vertical resistance of $2\Omega$. Therefore, it can be removed out of the circuit.

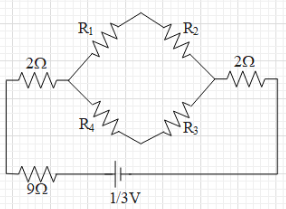
Now, we can see that both the pairs of $2\Omega$ resistances are series connections.
When two resistances are in series connection, the equivalent resistance of the two is given as ${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$.
Therefore, equivalent resistance of both the pairs is equal to $2+2=4\Omega$.

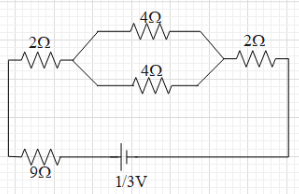
Now, the two $4\Omega$ resistances are parallel connections. When two resistances are in parallel connection the equivalent resistance of the two are given as ${{R}_{eq}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$.
Therefore, the equivalent resistance of these two is $\dfrac{(4)(4)}{4+4}=2\Omega$.

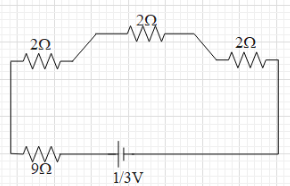
Now, we can see that three $2\Omega$ and one $9\Omega$ are in series connection. Therefore, the equivalent resistance of the circuit is ${{R}_{eq}}=2+2+2+9=15\Omega$.
(b) From Ohm’s law, we know that $\Delta V=i{{R}_{eq}}$, where i is the current passing through the battery and $\Delta V$ is the potential difference produced by the battery.
It is given that $\Delta V=\dfrac{1}{3}V$ and we found that ${{R}_{eq}}=15\Omega$.
$\Rightarrow \dfrac{1}{3}=i(15)$
$\Rightarrow i=\dfrac{1}{45}A$.
This current $i$ current is passing through the resistance of $9\Omega$. Therefore, the potential difference across this resistance is $\Delta V'=\dfrac{1}{45}\times 9=\dfrac{1}{5}=0.2V$
The potential difference between points A and B can be written as ${{V}_{A}}-{{V}_{B}}=\Delta V-\Delta V'$.
$\Rightarrow {{V}_{A}}-{{V}_{B}}=\dfrac{1}{3}-\dfrac{1}{5}\\\ \therefore{{V}_{A}}-{{V}_{B}}=\dfrac{2}{15}V$.

Note: There is always a drop in potential when we go from one end of a resistance to the other end, in the direction of the flow of the current. That is why when we go from point B to point A, first there is an increase in potential (due to the battery) and then there is decrease in the potential when we cross the resistance.