Question
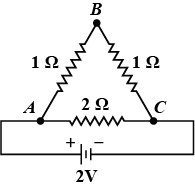
Question: For the given circuit, calculate (i) equivalent resistance between the points A and C. (ii) curr...
For the given circuit, calculate
(i) equivalent resistance between the points A and C.
(ii) current in the circuit
(iii) potential difference between A and B
Solution
(i) The resistance across AB and resistance across BC is in series and the equivalent resistance of these two will be parallel to the 2Ω resistance.
(ii) Find out the equivalent resistance of the circuit. Current across any resistance R is given by I=RV where V is the potential difference across the resistance.
(iii) Voltage or potential difference across resistors in parallel connection is same and current across resistors in series connection is same. Find the potential difference across AC and then current through ABC. Finally, the potential difference between A and B will be VAB=IRAB .
Complete step by step answer:
(i) As clear from the figure that both the 1Ω resistances are connected in series and we know that if two resistance are connected in series then their equivalent resistance is the algebraic sum of the two resistances. So, the equivalent resistance of the 1Ω resistances will be R1=1Ω+1Ω=2Ω .
Now, R1 will be parallel to the 2Ω resistance. So, the equivalent resistance across AC will be
RAC=2+22×2=1Ω
Hence, the equivalent resistance between the points A and C is 1Ω .
(ii) To find the current in the circuit, we have to first calculate the equivalent resistance of the circuit.
The equivalent resistance of the circuit is 1Ω .
We know that the current across any resistance R is given by I=RV where V is the potential difference across the resistance.
So, the current through the circuit
I=12=2A .
(iii) As clear from the figure that both the 1Ω resistances are connected in series and they are parallel with the 2Ω resistance. We know that the voltage or potential difference across resistors in parallel connection is the same and current across resistors in series connection is the same.
So, the potential difference across the equivalent resistance R1=2Ω is V=2V .
Therefore, current through ABC will be I=22=1Ω .
Now, the potential difference between A and B will be VAB=IRAB
So, VAB=1×1=1V
Hence, the potential difference between A and B is 1V .
Note: The relation between current and voltage is explained by the Ohm’s Law which states that the amount of electric current passing through a conductor in a circuit is directly proportional to the voltage or potential difference across it, at a fixed temperature and similar physical conditions.
