Question

For the function $f(x) = (x^2 + bx + c)e^x$ and $g(x) = (x^2 + bx + c)e^x + e^{x(2x + b)}$. Which of the following holds good?

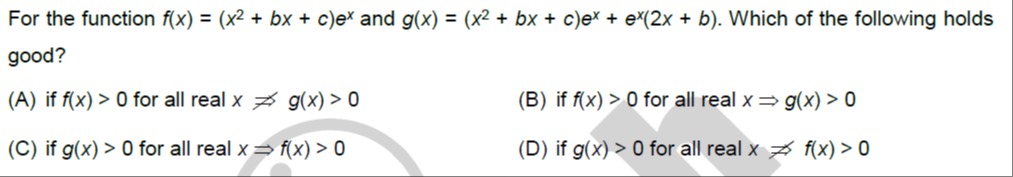
• A. if $f(x) > 0$ for all real $x \nRightarrow g(x) > 0$
• B. if $f(x) > 0$ for all real $x \Rightarrow g(x) > 0$
• C. if $g(x) > 0$ for all real $x \Rightarrow f(x) > 0$
• D. if $g(x) > 0$ for all real $x \nRightarrow f(x) > 0$

Answer 1

Answer: (B)

if $f(x) > 0$ for all real $x \Rightarrow g(x) > 0$

Answer 2

Given $f(x) = (x^2 + bx + c)e^x$ and $g(x) = (x^2 + bx + c)e^x + e^{x(2x + b)}$, we can rewrite $g(x)$ as $g(x) = f(x) + e^{x(2x + b)}$.

Since $e^{x(2x + b)} > 0$ for all real $x$, if $f(x) > 0$ for all real $x$, then $g(x) = f(x) + e^{x(2x + b)} > 0$ for all real $x$.

Therefore, if $f(x) > 0$ for all real $x$, then $g(x) > 0$ for all real $x$.