Question

For the function $f(x) = \frac{ln(x)}{x}$, what is $f'(x)$?

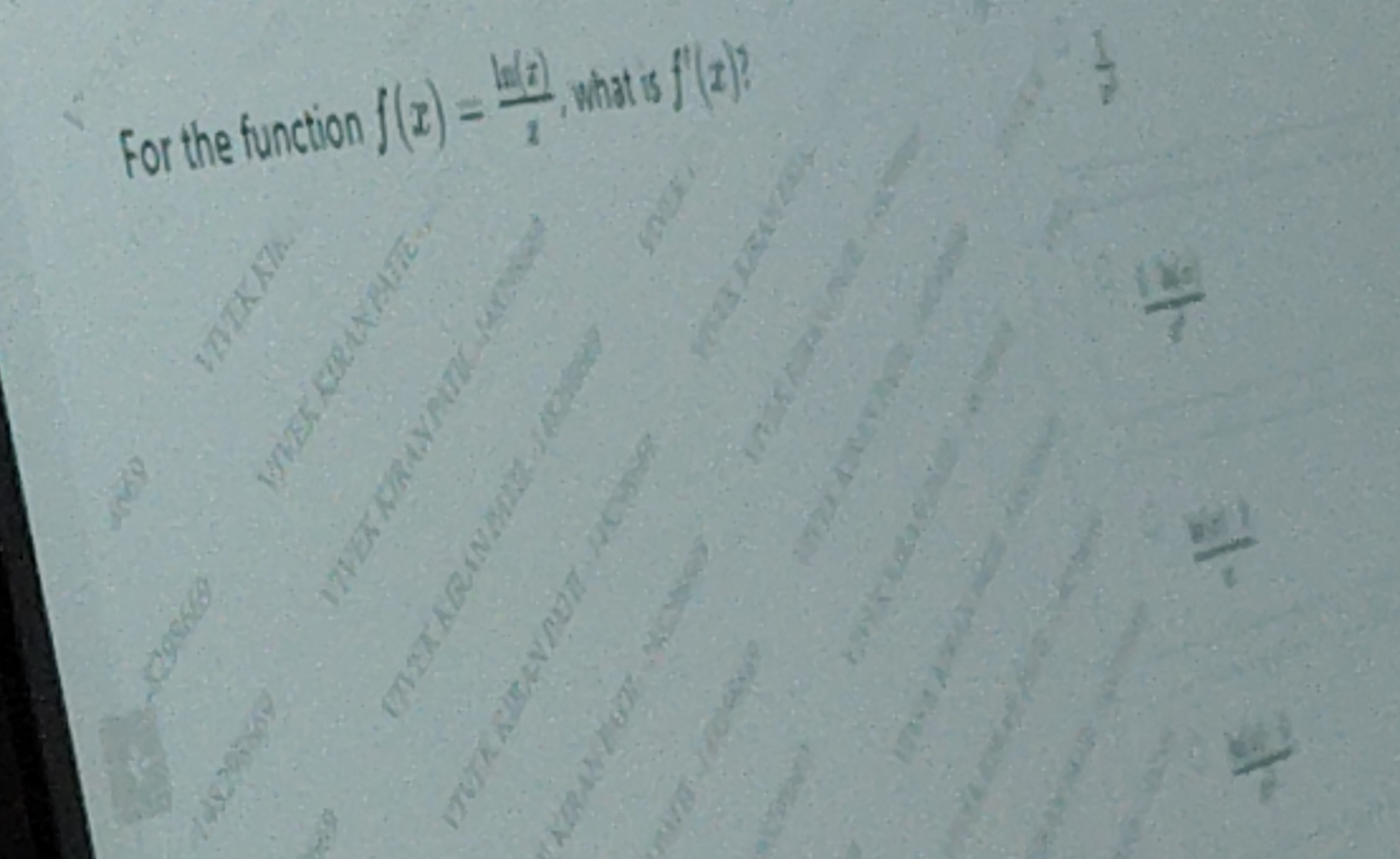
• A. $\frac{1}{x}$
• B. $\frac{ln}{x}$
• C. $\frac{1}{x}$

Answer 1

$\frac{1 - \ln(x)}{x^2}$

Answer 2

The function given is $f(x) = \frac{\ln(x)}{x}$. We need to find its derivative, $f'(x)$.

To differentiate this function, we use the quotient rule, which states that if $f(x) = \frac{u(x)}{v(x)}$, then $f'(x) = \frac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2}$.

In this case:

Let $u(x) = \ln(x)$ Let $v(x) = x$

Now, we find the derivatives of $u(x)$ and $v(x)$: $u'(x) = \frac{d}{dx}(\ln(x)) = \frac{1}{x}$ $v'(x) = \frac{d}{dx}(x) = 1$

Substitute these into the quotient rule formula: $f'(x) = \frac{\left(\frac{1}{x}\right) \cdot (x) - (\ln(x)) \cdot (1)}{x^2}$ $f'(x) = \frac{1 - \ln(x)}{x^2}$

This is the derivative of the given function.