Question

For the first order reaction, ${\text{2 }}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{ }}\left( {\text{g}} \right){\text{ }} \to {\text{ 4 N}}{{\text{O}}_{\text{2}}}\left( {\text{g}} \right){\text{ + }}{{\text{O}}_{\text{2}}}\left( {\text{g}} \right)$ .This question has multiple correct options
A The concentration of the reactant decreases exponentially with time
B the half-life of the reaction decreases with increasing temperature
C the half-life of the reaction depends on the initial concentration of the reactant
D the reaction proceeds to 99.6% completion in eight half-life duration

Answer 1

For a first order reaction, the rate of the reaction is directly proportional to the reactant concentration. The half-life period represents the time required for the ${\text{50\% }}$ change in the reactant concentration.

Complete Step by step answer: For the first order reaction, ${\text{2 }}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}{\text{ }}\left( {\text{g}} \right){\text{ }} \to {\text{ 4 N}}{{\text{O}}_{\text{2}}}\left( {\text{g}} \right){\text{ + }}{{\text{O}}_{\text{2}}}\left( {\text{g}} \right)$ .
The concentration of the reactant dinitrogen pentoxide decreases exponentially with time
For the first order reaction, $\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right] = {\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right]_0}{e^{ - kt}}$

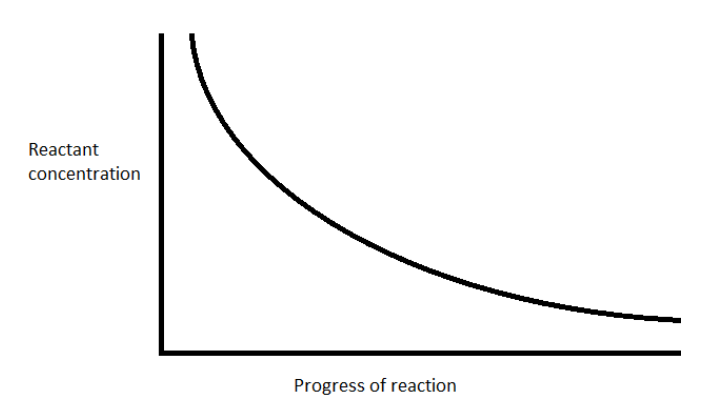
Hence, the option (A) represents the correct option.
B the half-life of the reaction decreases with increasing temperature
For the first order reaction the half-life period ${t_{1/2}}$ , is independent of the initial concentration of reactants.
${t_{1/2}} = \dfrac{{0.693}}{k}$
The half life period is inversely proportional to the rate constant.
The specific reaction rate or the rate constant $k$ is constant for the reaction at a constant temperature. The rate constant changes either with temperature or with presence of a catalyst.
With increase in the temperature, the value of the rate constant increases and the value of the half life period decreases.
Hence, the option (B) represents the correct option
For the first order reaction the half-life period ${t_{1/2}}$ , is independent of the initial concentration of reactants.
${t_{1/2}} = \dfrac{{0.693}}{k}$
Hence, the option (C) represents the incorrect option.
The reaction proceeds to 99.6% completion in eight half-life duration
After n half life periods,
$\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right] = \dfrac{{{{\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right]}_0}}}{{{2^n}}}$
After 8 half life periods,
$\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right] = \dfrac{{{{\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right]}_0}}}{{{2^8}}}$
Calculate the percentage completion after 8 half-life periods
$\dfrac{{\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right] - \dfrac{{{{\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right]}_0}}}{{{2^8}}}}}{{{{\left[ {{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}} \right]}_0}}} \times 100 = 99.6\%$

Hence, the options (A) and (D) represent the correct option.

Note: If you know the half-life period for the first order reaction, you can calculate the rate constant. For this, you can plot a graph of reactant concentrations and different time instances. Then from the graph, you can determine the time needed for the concentration to reduce to one half.