Question
Question: For the figure $\vec{A} + \vec{B} = \vec{C}$ $\vec{B} + \vec{C} = \vec{A}$ $\vec{C} + \vec{A} = \...
For the figure
A+B=C
B+C=A
C+A=B
X
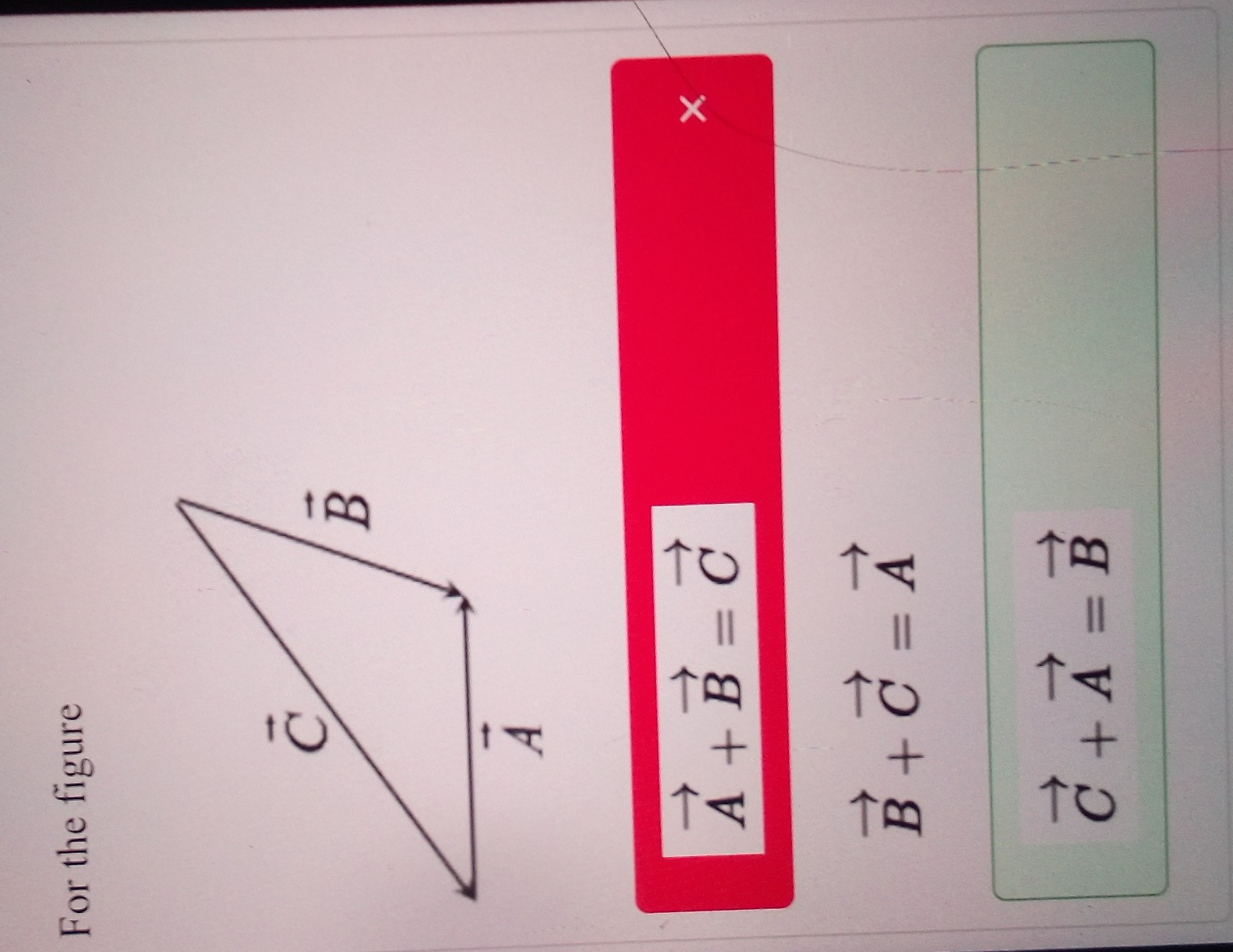
A+B=C
Solution
The figure displays three vectors A, B, and C forming a triangle. To determine the correct vector sum, we apply the triangle law of vector addition.
The triangle law states that if two vectors are represented by two sides of a triangle taken in the same order, their resultant is represented by the third side taken in the opposite order.
Let's trace the vectors in the figure:
- Vector A starts from the bottom-left vertex and points to the bottom-right vertex.
- Vector B starts from the head of A (bottom-right vertex) and points to the top vertex.
- Vector C starts from the tail of A (bottom-left vertex) and points to the head of B (top vertex).
According to the triangle law of vector addition: If we add A and B (which are taken in the same order, head-to-tail), their resultant vector should start from the tail of A and end at the head of B. Observing the figure, the vector C precisely matches this description: it starts at the tail of A and ends at the head of B.
Therefore, the correct vector equation is: A+B=C
Let's verify the other options:
- B+C=A: For this to be true, B and C must be head-to-tail, and A must be the resultant. In the figure, B and C are not arranged head-to-tail. Specifically, the head of B and the head of C meet at the top vertex, and the tail of B is the head of A, while the tail of C is the tail of A. This equation is incorrect.
- C+A=B: For this to be true, C and A must be head-to-tail, and B must be the resultant. In the figure, the head of C is at the top vertex, and the tail of A is at the bottom-left vertex. They are not connected head-to-tail. This equation is incorrect.
Thus, only the first statement is correct based on the given figure.
