Question

For the ellipse given, $\dfrac{{{{\left( {x - 3} \right)}^2}}}{{25}} + \dfrac{{{{\left( {y - 2} \right)}^2}}}{{16}} = 1$, match the equations of the lines given in the list I and list II.

List I	List II
i) the equation of the major axis	(a) 3x = 34
ii) the equation of a directrix	(b) y = 2
iii) the equation of latus rectum	(c) x + y = 0
(d) x = 6
(e) x = 3
(f) 3y = 34

$\left( a \right)$ i) – e, ii) – a, iii) – d
$\left( b \right)$ i) – b, ii) – f, iii) – e
$\left( c \right)$ i) – b, ii) – a, iii) – e
$\left( d \right)$ i) – b, ii) – a, iii) – d

Answer 1

In this particular question use the concept that the standard equation of ellipse centered at (h, k) is given as, $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$, where a and b are the lengths of semi major and semi minor axis respectively and use that if a > b then the equation of the major axis of the ellipse is parallel to the x-axis and passing through the center of the ellipse, so use these concepts to reach the solution of the question.

Complete step by step answer:
Given equation of ellipse
$\dfrac{{{{\left( {x - 3} \right)}^2}}}{{25}} + \dfrac{{{{\left( {y - 2} \right)}^2}}}{{16}} = 1$
Now compare with the standard equation of the ellipse $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$, where (h, k) is the center of the ellipse and a and b are the lengths of semi major and semi minor axis respectively.
So on comparing we have,
$\Rightarrow h = 3,k = 2,{a^2} = 25,{\text{ and }}{b^2} = 16$
$\Rightarrow h = 3,k = 2,a = 5,{\text{ and }}b = 4$
So the center of the ellipse is (h, k) = (3, 2)

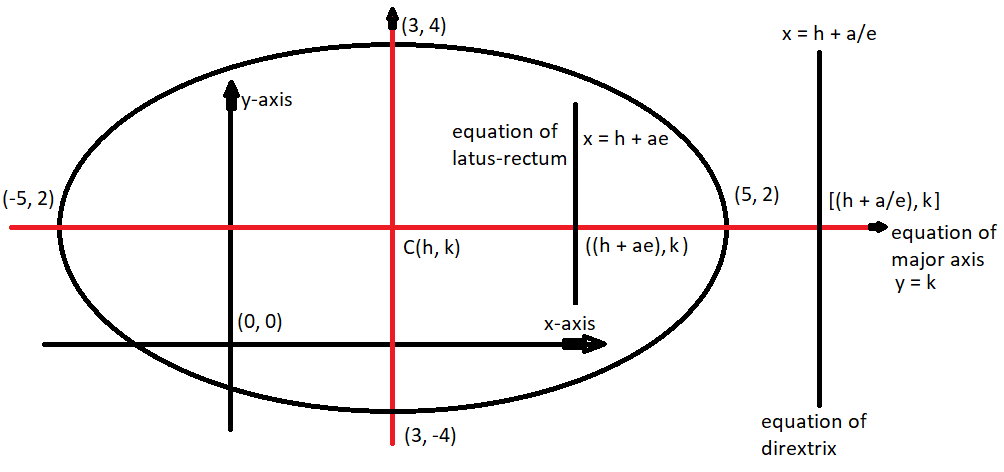
And as we see that a > b, so the equation of the major axis is parallel to the x-axis and passes through the center of the ellipse.
So the equation of the major axis parallel to the x-axis and passing through point (3, 2) is, y = 2 as shown in the above figure.
So the equation of the major axis of the ellipse is, y = 2.
Now as we know that the eccentricity e, of the ellipse is calculated as,
$\Rightarrow {b^2} = {a^2}\left( {1 - {e^2}} \right)$, Where symbols have their usual meaning.
$\Rightarrow 16 = 25\left( {1 - {e^2}} \right)$
$\Rightarrow \left( {1 - {e^2}} \right) = \dfrac{{16}}{{25}}$
$\Rightarrow {e^2} = 1 - \dfrac{{16}}{{25}} = \dfrac{9}{{25}}$
$\Rightarrow e = \sqrt {\dfrac{9}{{25}}} = \dfrac{3}{5}$
Now the directrix of the ellipse is at distance (a/e) from the center, so the coordinates of the directrix is given as, [(h + a/e), k].
So the equation of the directrix of the ellipse is, x = h + a/e as shown in the above figure.
$\Rightarrow x = 3 + \dfrac{5}{{\dfrac{3}{5}}} = 3 + \dfrac{{25}}{3}$
$\Rightarrow x = \dfrac{{34}}{3}$
$\Rightarrow 3x = 34$
So this is the equation of the directrix.
Now as we know that the latus rectum of the ellipse is always passing through the focus of the ellipse.
So the latus rectum of the ellipse is at distance (ae) from the center, so the coordinates of the latus rectum/focus is given as, [(h + ae), k].
So the equation of the latus rectum of the ellipse is, x = h + ae as shown in the above figure.
$\Rightarrow x = 3 + 5\left( {\dfrac{3}{5}} \right) = 3 + 3 = 6$
$\Rightarrow x = 6$
So this is the equation of the latus rectum.
Hence option (d) is the correct answer.
Note:
Whenever we face such types of questions the key concept we have to remember is that always recall the standard equation of ellipse which is stated above, and always recall that the directrix of the ellipse is at distance (a/e) from the center, so the coordinates of the directrix is given as, [(h + a/e), k] and the latus rectum of the ellipse is at distance (ae) from the center, so the coordinates of the latus rectum/focus is given as, [(h + ae), k].