Solveeit Logo
Login

Question

Question: For the difference amplifier circuit shown, determine the output voltage at terminal \(A\). A. \( ...

For the difference amplifier circuit shown, determine the output voltage at terminal AA.
A. −18.13  V - 18.13\;{\rm{V}}.
B. −6.07  V - 6.07\;{\rm{V}}.
C. 6.07  V6.07\;{\rm{V}}.
D. 15.45  V15.45\;{\rm{V}}.

Explanation

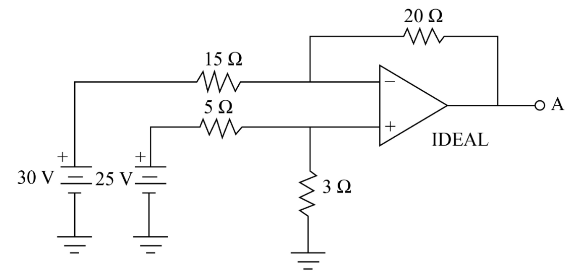
Solution

In this solution we will take the equivalent resistance when the resistances are connected in the parallel or series connection and will take the voltages of voltmeters to find out the output voltage at the given terminal.

Complete step by step answer:
Voltage V1=30  V{V_1} = 30\;{\rm{V}}.
Voltage V2=25  V{V_2} = 25\;{\rm{V}}.
Resistance R1=15  Ω{R_1} = 15\;\Omega .
Resistance R2=20  Ω{R_2} = 20\;\Omega .
Resistance R3=5  Ω{R_3} = 5\;\Omega .
Resistance R4=3  Ω{R_4} = 3\;\Omega .
When a circuit or device has a power gain more than one then that circuit is known as an amplifier. The amplifiers are mostly used in the electronic components.
Express the formula of the output voltage of the difference amplifier.
VA=−R2R1V1+(R4R3+R4)(1+R2R1)V2{V_A} = - \dfrac{{{R_2}}}{{{R_1}}}{V_1} + \left( {\dfrac{{{R_4}}}{{{R_3} + {R_4}}}} \right)\left( {1 + \dfrac{{{R_2}}}{{{R_1}}}} \right){V_2}
Here,
VA{V_A} is the voltage at AA.
R2{R_2},R1{R_1},R3{R_3} and R4{R_4} are the resistance.
V1V{}_1 and V2{V_2} are the voltage.
Substitute 30  V30\;{\rm{V}} for V1{V_1} , 25  V25\;{\rm{V}} for V2{V_2} , 15  Ω15\;\Omega for R1{R_1} , 20  Ω20\;\Omega for R2{R_2}, 5  Ω5\;\Omega for R3{R_3} and 3  Ω3\;\Omega for R4{R_4} to obtain the voltage at AA.
VA=−20  Ω15  Ω(30  V)+(3  Ω3  Ω+5  Ω)(1+20  Ω15  Ω)(25  V) ⇒VA=−40+2125(25  V) ⇒VA=−40+52524    V ⇒VA=−40+21.875  V ⇒VA=−18.125  V ∴VA=−18.13  V {V_A} = - \dfrac{{20\;\Omega }}{{15\;\Omega }}\left( {30\;{\rm{V}}} \right) + \left( {\dfrac{{3\;\Omega }}{{3\;\Omega + 5\;\Omega }}} \right)\left( {1 + \dfrac{{20\;\Omega }}{{15\;\Omega }}} \right)\left( {25\;{\rm{V}}} \right)\\\ \Rightarrow{V_A} = - 40 + \dfrac{{21}}{{25}}\left( {25\;{\rm{V}}} \right)\\\ \Rightarrow{V_A} = - 40 + \dfrac{{525}}{{24}}\;\;{\rm{V}}\\\ \Rightarrow{V_A} = - 40 + 21.875\;{\rm{V}}\\\ \Rightarrow {V_A} = - 18.125\;{\rm{V}}\\\ \therefore{V_A} = - 18.13\;{\rm{V}}
Therefore, the correct option is (A).

Note: While solving this type of questions make sure that the prediction of parallel or series connection must be right to find out the equivalent resistance otherwise the solution will be wrong.