Question

For the curve with equation $y=\sqrt{x}-1$ and the straight line with equation $y=kx$, find the values of k such that:
a) The line meets the curve twice
b) The line meets the curve once

Answer 1

From the question we have been given a curve and a straight line and asked to find the value of k for given conditions. For this we will equate the both curve and line and simplify them and bring a quadratic equation. From that quadratic equation which we got we will use the discriminant of quadratic equation and get the solutions in both cases.

Complete step by step answer:
Firstly, as mentioned above we will equate the both curved and straight line. So, we get,
$\Rightarrow \sqrt{x}-1=kx$
Now, we will bring one to the other side of the equation. We get,
$\Rightarrow \sqrt{x}=kx+1$
Now, we will square on both sides of the equation that is the right hand and left hand side of the equation. So, we get,
$\Rightarrow {{\left( kx+1 \right)}^{2}}=x$
$\Rightarrow {{\left( kx \right)}^{2}}+2kx+1=x$
$\Rightarrow {{\left( kx \right)}^{2}}+(2k-1)x+1=0$
Here we got a quadratic equation.
Now, for the case where one line meets the curve twice, then the discriminant of the quadratic equation must be greater than zero.
So, we have the discriminant as follows.
For, case 1 the $\Rightarrow \Delta >0$ so,
For a quadratic equation we have $\Rightarrow \Delta ={{b}^{2}}-4ac$.so,
$\Rightarrow \Delta ={{b}^{2}}-4ac$
$\Rightarrow \Delta ={{\left( 2k-1 \right)}^{2}}-4{{k}^{2}}$
$\Rightarrow {{\left( 2k-1 \right)}^{2}}-4{{k}^{2}}>0$
$\Rightarrow 4{{k}^{2}}-4k+1-4{{k}^{2}}>0$
$\Rightarrow 4k<1$
$\Rightarrow k<\dfrac{1}{4}$
The figure when we take $k=-1$ will be as follows.

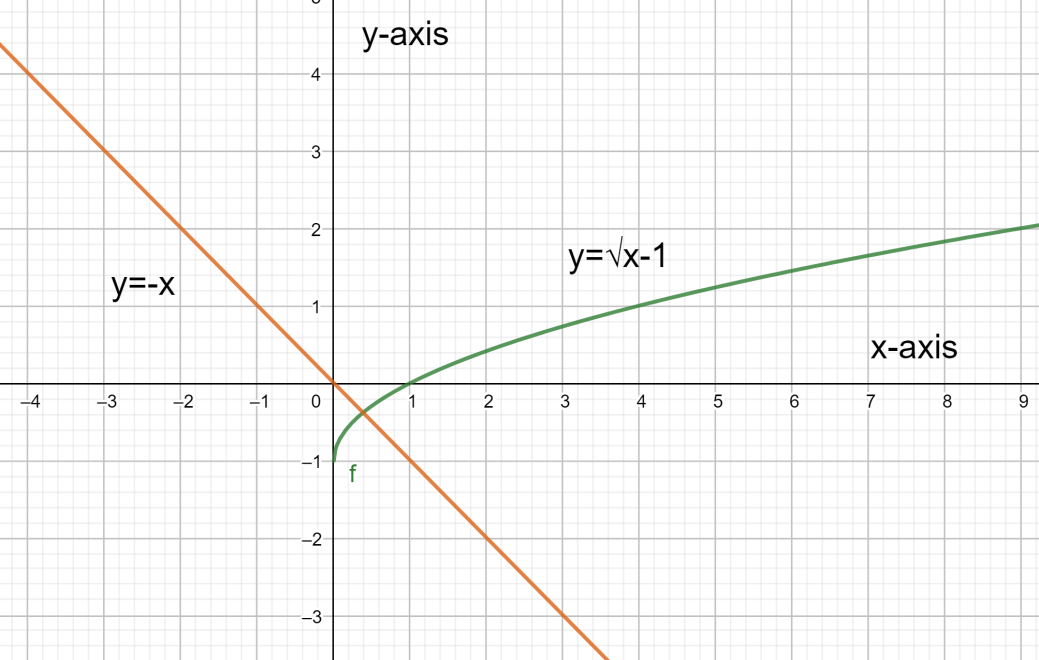
For the second case the $\Delta =0$
So, we get,
$\Rightarrow \Delta ={{b}^{2}}-4ac$
$\Rightarrow \Delta ={{\left( 2k-1 \right)}^{2}}-4{{k}^{2}}$
$\Rightarrow {{\left( 2k-1 \right)}^{2}}-4{{k}^{2}}=0$
$\Rightarrow 4{{k}^{2}}-4k+1-4{{k}^{2}}=0$
$\Rightarrow k=\dfrac{1}{4}$
When we take $\Rightarrow k=\dfrac{1}{4}$ the figure will be as follows.

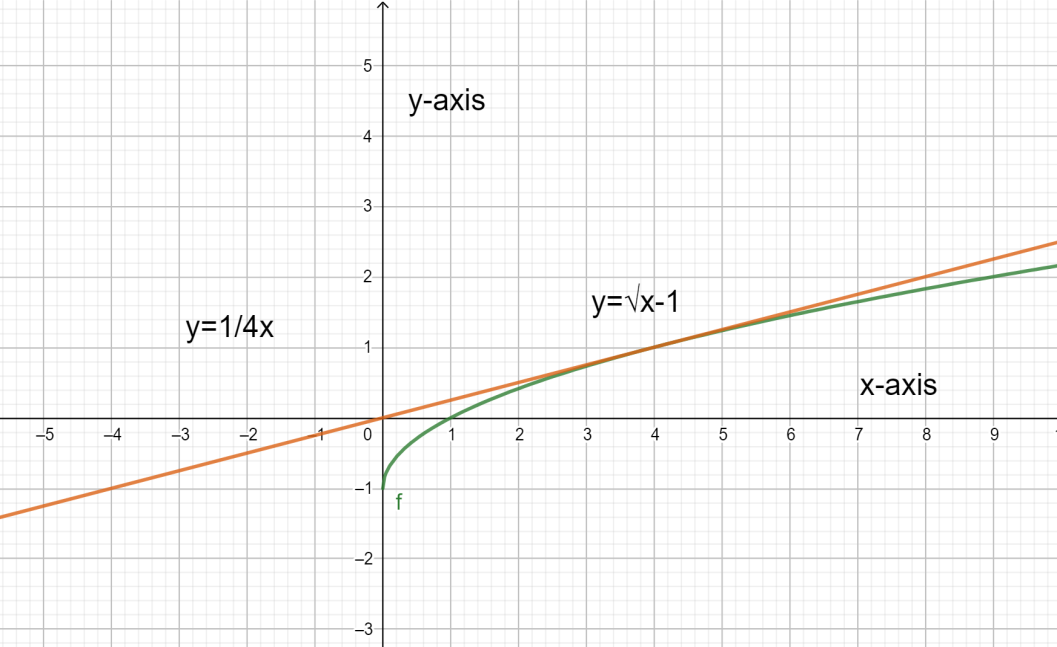
Therefore, for the given question the line meets curve twice when $\Rightarrow k<\dfrac{1}{4}$ and the line meets the curve once when $\Rightarrow k=\dfrac{1}{4}$.

Note: Students must be very careful in doing the simplifications. Students must have good knowledge in quadratic equations and its applications. Students should know the formula for discriminate which is $\Rightarrow \Delta ={{b}^{2}}-4ac$. Students should not make mistakes for example in the first case if we write $\Rightarrow \Delta <0$ instead of $\Rightarrow \Delta >0$ our solution will be wrong.