Question
Question: For the current-carrying wire as shown, the magnetic field at P is:...
For the current-carrying wire as shown, the magnetic field at P is:
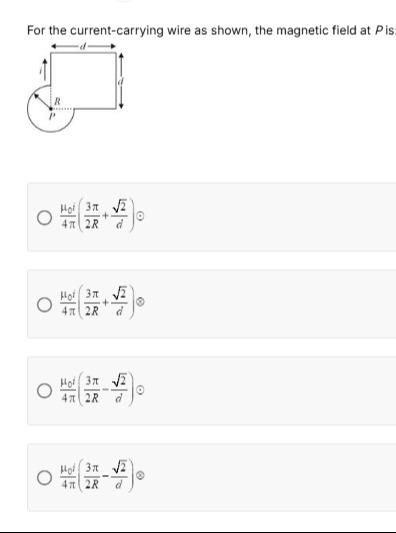
\frac{\mu_0i}{4\pi}(\frac{3\pi}{2R}+\frac{\sqrt{2}}{d})\bigotimes
\frac{\mu_0i}{4\pi}(\frac{3\pi}{2R}+\frac{\sqrt{2}}{d})\bigotimes
\frac{\mu_0i}{4\pi}(\frac{3\pi}{2R}-\frac{\sqrt{2}}{d})\bigotimes
\frac{\mu_0i}{4\pi}(\frac{3\pi}{2R}-\frac{\sqrt{2}}{d})\bigotimes
\frac{\mu_0i}{4\pi}(\frac{3\pi}{2R}+\frac{\sqrt{2}}{d})\bigotimes
Solution
The magnetic field at point P is the sum of contributions from the curved part and the straight part of the wire. The term 4πμ0i2R3π suggests a contribution from a curved segment. If we assume this segment is a circular arc subtending an angle θ at the center, the magnetic field at the center is given by Bcurved=4πRμ0iθ. For this term to match, θ=23π. This implies the curved part is a 3/4 circular arc. The direction of the magnetic field at the center of a clockwise current loop is into the page (⨂).
The term 4πμ0id2 suggests a contribution from a straight wire segment of length related to d. The exact geometry for this term is not explicitly defined but is assumed to contribute to the field at P. The direction of this contribution is also into the page (⨂).
Since both contributions are into the page, they add up. Total magnetic field B=Bcurved+Bstraight=4πμ0i2R3π+4πμ0id2=4πμ0i(2R3π+d2).
