Question

For the current carrying loop shown, the net magnetic field at the centre of the circle $O$ due to it, for $\theta < {180^ \circ }$ is $B$. Then $B$ is,

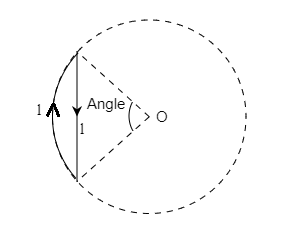
(A) perpendicular to paper inwards
(B) perpendicular to paper outwards
(C) perpendicular to paper inwards if $\theta \leqslant {90^ \circ }$ and perpendicular to paper outwards if ${90^ \circ } \leqslant \theta \leqslant {180^ \circ }$
(D) None of them

Answer 1

The solution of this question is given by Maxwell's right hand thumb rule. By using this right-hand thumb rule, the direction of the magnetic field and the current is determined by using the direction shown in the figure.

Complete step by step solution:
According to this rule, if we hold the current carrying wire in our right hand so that our thumb points in the direction of current, the direction in which our fingers will give the direction of magnetic field lines around the wire. When the thumb points upwards, the fingers are anticlockwise.

For this figure circuit carrying loop shown in the figure, the net magnetic field at the centre of the circle $O$ due to it, for $\theta < {180^ \circ }$ is $B$, then $B$ is, calculation of in the field due to the two segments and add them up. The direction of the field due to the circular part of the loop in perpendicular to the paper inwards and due to the straight portion of loop is outwards. They will be in opposite directions and the field due to the straight wire dominates as it nears the centre $O$.

Hence, the option (B) is the correct answer.

Note: The direction of the current in the circular loop is anticlockwise, by this the direction of $B$ acts perpendicular to paper inwards. But the direction of current in a straight line is very close to the centre point $O$, so it dominates, so the direction of $B$ acts perpendicular to paper outwards.