Question

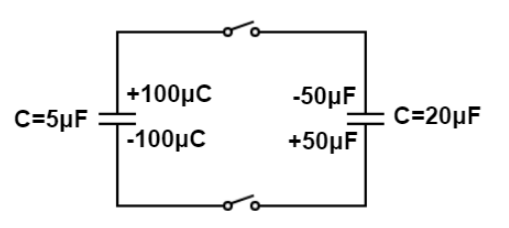
: For the configuration of capacitors shown, both switches are closed simultaneously. After equilibrium is established, what is the charge on the top plate of the $5\mu F$ capacitor?

A. $100\mu C$
B. $90\mu C$
C. $10\mu C$
D. None of these

Answer 1

In order to solve this question, we will first calculate the total charge distributed on upper plate of both capacitors and then by using the concept that both capacitors are connected in parallel so that their potential difference will be same and hence, by forming equation in form of charge on both capacitors we will calculate the charge on the top plate of the $5\mu F$ capacitor.

Complete answer:
According to the given diagram, the total charge distributed on the upper plate is simply the sum of $100\mu C - 50\mu C = + 50\mu C \to (i)$ .
Now, from the diagram we see that, Both capacitors are connected in parallel combination and let ${Q_5},{Q_{20}}$ denotes the charge on capacitors of $5\mu F{\kern 1pt} {\kern 1pt} and{\kern 1pt} {\kern 1pt} 20\mu F$ and both capacitors will have same potential difference and the relation between capacitance, voltage and charge is calculated as
$V = \dfrac{Q}{C}$ so for each capacitance we have,
$\Rightarrow V = \dfrac{{{Q_5}}}{5}$ and $V = \dfrac{{{Q_{20}}}}{{20}}$ so we get,
$\Rightarrow \dfrac{{{Q_5}}}{5} = \dfrac{{{Q_{20}}}}{{20}}$
$\Rightarrow {Q_{20}} = 4{Q_5} \to (ii)$

And from equation (i) we have, ${Q_5} + {Q_{20}} = 50\mu C$ as total charge distributed among both capacitors.
Put the value of ${Q_{20}} = 50\mu C - {Q_5}$ in equation (ii) we get,
$4{Q_5} = 50\mu C - {Q_5}$
$\Rightarrow 5{Q_5} = 50\mu C$
$\therefore {Q_5} = 10\mu C$
So, charge on the $5\mu F$ capacitor will be ${Q_5} = 10\mu C$.

Hence, the correct option is C.

Note: It should be remembered that, the actual total charge on both capacitor can be written just the sum of charge stored in each capacitor but here, we just take the value of charge on the upper plate of each capacitor, Unit of capacitance is related as $1\mu F = {10^{ - 6}}F$ and unit of charge is related as $1\mu C = {10^{ - 6}}C$.