Question

For the combination of two thin lenses are given in List I. The radius of curvature of all curved surfaces is $r$ and the refractive index of all the lenses is $1.5$. Match lens combinations in List I with their focal length in List II:

List I	List II
P.	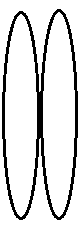1. $2r$
Q.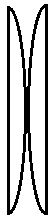	2. $r/2$
R.	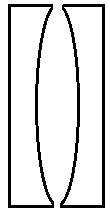3. $- r$
S.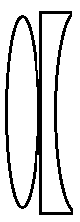	4. $r$

(A) P-1, Q-2, R-3, S-4
(B) P-2, Q-4, R-3, S-1
(C) P-4, Q-1, R-2, S-3
(D) P-2, Q-1, R-3, S-4

Answer 1

To solve this problem, we need to find the local length of each lens individually from the combinations. Then using the lens maker’s formula, we need to find the focal length of each combination in List I and match them to List II.

Formula used:
In this solution we will be using the following formula,
$\Rightarrow \dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
where $f$ is the focal length, $\mu$ is the refractive index
$\Rightarrow {R_1},{R_2}$are the radius of the circles of which the lens are a part
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
where ${f_1}$ and ${f_2}$ are the focal length of the lenses in the combination.

Complete step by step solution:
To find the focal lengths of each of the combinations, we use the following method.
Let us consider the first combination at P.
Here for 1 lens, the radius of curvature of both the surfaces are $r$. So the focal length of the one of the lens will be given by the formula, $\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ {\dfrac{1}{r} + \dfrac{1}{r}} \right]$
So we get, $\dfrac{1}{f} = 0.5 \times \dfrac{2}{r}$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{1}{r}$
So the focal length of both the lens in the combination is ${f_1} = {f_2} = r$
So from the lens maker’s formula, substituting we get
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{r} + \dfrac{1}{r}$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{2}{r}$
So the focal length is $f = \dfrac{r}{2}$
Now let us consider the combination in Q.
Here for 1 lens, the radius of curvature of one of the surfaces is $r$and the other surface is $\infty$ . So the focal length of the one of the lens will be given by the formula, $\Rightarrow \dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ {\dfrac{1}{\infty } + \dfrac{1}{r}} \right]$
So we get, $\dfrac{1}{f} = 0.5 \times \dfrac{1}{r}$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{{0.5}}{r}$
So the focal length of both the lens in the combination is ${f_1} = {f_2} = \dfrac{r}{{0.5}}$
So from the lens maker’s formula, substituting we get
$\Rightarrow \dfrac{1}{f} = \dfrac{{0.5}}{r} + \dfrac{{0.5}}{r}$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{1}{r}$
So the focal length is $f = r$
Now let us consider the combination in R.
Here for 1 lens, the radius of curvature of one of the surfaces is $- r$and the other surface is $\infty$ . So the focal length of the one of the lens will be given by the formula, $\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ {\dfrac{1}{\infty } - \dfrac{1}{r}} \right]$
So we get, $\dfrac{1}{f} = - 0.5 \times \dfrac{1}{r}$
Hence on calculating we get, $\dfrac{1}{f} = - \dfrac{{0.5}}{r}$. So ${f_1} = - \dfrac{r}{{0.5}}$
Here for the second lens, the radius of curvature of one of the surfaces is $- \infty$ and the other surface is $- r$ . So the focal length of the one of the lens will be given by the formula, $\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ { - \dfrac{1}{r} - \dfrac{1}{\infty }} \right]$
So we get, $\dfrac{1}{f} = - 0.5 \times \dfrac{1}{r}$
Hence on calculating we get, $\dfrac{1}{f} = - \dfrac{{0.5}}{r}$
So the focal length of both the lens in the combination is ${f_1} = {f_2} = - \dfrac{r}{{0.5}}$
So from the lens maker’s formula, substituting we get
$\Rightarrow \dfrac{1}{f} = - \left( {\dfrac{{0.5}}{r} + \dfrac{{0.5}}{r}} \right)$
Hence on calculating we get, $\dfrac{1}{f} = - \dfrac{1}{r}$
So the focal length is $f = - r$
Now let us consider the combination in S.
Here for 1 lens, the radius of curvature of one of the surfaces is $r$and the other surface is $- r$ . So the focal length of the one of the lens will be given by the formula, $\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ {\dfrac{1}{r} + \dfrac{1}{r}} \right]$
So we get, $\dfrac{1}{f} = 0.5 \times \dfrac{2}{r}$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{1}{r}$. So ${f_1} = r$
Here for the second lens, the radius of curvature of one of the surfaces is $\infty$ and the other surface is $r$ . So the focal length of the one of the lens will be given by the formula, $\Rightarrow \dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right]$
Substituting $\mu = 1.5$ we get,
$\Rightarrow \dfrac{1}{f} = \left( {1.5 - 1} \right)\left[ {\dfrac{1}{\infty } - \dfrac{1}{r}} \right]$
So we get, $\dfrac{1}{f} = - 0.5 \times \dfrac{1}{r}$
Hence on calculating we get, $\dfrac{1}{f} = - \dfrac{{0.5}}{r}$
So the focal length of the lens in the combination are ${f_1} = r$ and ${f_2} = - \dfrac{r}{{0.5}}$
So from the lens maker’s formula, substituting we get
$\Rightarrow \dfrac{1}{f} = \left( {\dfrac{1}{r} - \dfrac{{0.5}}{r}} \right)$
Hence on calculating we get, $\dfrac{1}{f} = \dfrac{{0.5}}{r}$
So the focal length is $f = 2r$
So the correct combinations in List I and List II are P-2, Q-4, R-3, S-1
So, the correct answer is option (B).

Note:
A convex lens is known as a converging lens since it converges the rays of light which are falling on it. Similarly a concave lens is also known as a diverging lens as it diverges the rays of light which fall on it.