Question
Question: For the combination of resistors shown in the figure, find the equivalent resistance between (a) \(C...
For the combination of resistors shown in the figure, find the equivalent resistance between (a) C and D (b) A and B.
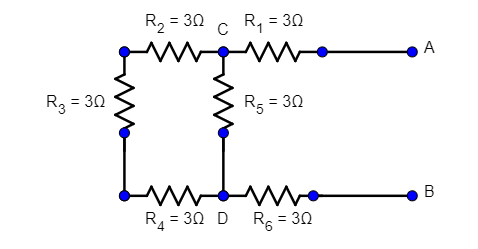
Solution
This problem can be solved by using the formulas for equivalent resistances for series and parallel combinations of resistances. For finding the equivalent resistance between two terminals, we have to find the equivalent resistance in all branches of the circuit between the two terminals.
Formula used:
Requivalent,series=i=1∑kRi
Requivalent,parallel1=i=1∑kRi1
Complete step-by-step answer:
We will have to solve the problem by using the formulas for the equivalent resistances for series and parallel combinations for all the branches between the two given terminals.
The equivalent resistance Requivalent,series of k resistances in series of individual resistances Ri(i∈[1,k]) is given by
Requivalent,series=i=1∑kRi --(1)
The equivalent resistance Requivalent,parallel of k resistances in parallel of individual resistances Ri(i∈[1,k]) is given by
Requivalent,parallel1=i=1∑kRi1 --(2)
Here R1=R2=R3=R4=R5=R6=3Ω
(a) Equivalent resistance between C and D -
The branches connecting C and D are the two branches, one containing R5 and the other containing resistors R2,R3,R4.
The other branch that is the one having nodes A and B is a broken circuit. Hence, R1,R6 are not considered for the equivalent resistance.
Therefore, the equivalent resistance is the parallel combination of the two branches, one containing R5 and the other containing resistors R2,R3,R4.
∴RCD=R2,3,4∣∣R5 --(3)
Now, R2,R3,R4 are in series. Therefore using (1) their equivalent will be
R2,3,4=R2+R3+R4=3+3+3=9Ω --(4)
Now, R2,3,4 and R5 are in parallel.
Therefore using (2), we get, the equivalent resistance between C and D as
RCD1=R51+R2,3,41=31+91=93+1=94
∴RCD=49=2.25Ω --(5)
(b) Equivalent resistance between A and B
For the equivalent resistance between A and B, we see that (R1),((R2+R3+R4)∣∣R5),R6 are in series, where
R2+R3+R4=R2,3,4 is the series combination of
R2,R3,R4.
Therefore using (1), we get, the equivalent resistance between A and B as
RAB=R1+(R2,3,4∣∣R5)+R6
∴RAB=3+2.25+3=8.25Ω [Using (3) and (5)]
∴RAB=8.25Ω
Note: Students should take care between which two terminals the equivalent resistance is being asked to find because as is evident from the above question, the equivalent resistance changes depending upon between which two terminals the equivalent resistance is being calculated. Sometimes questions are given in such a way that the student jumps to conclusions and starts to calculate the equivalent resistance between one set of terminals but the question actually asks for the equivalent resistance between a completely different set of terminals.
