Question
Question: For the circuit shown, what is the current (in mA) in the ideal inductor when the current in the bat...
For the circuit shown, what is the current (in mA) in the ideal inductor when the current in the battery is 0.50A in the direction shown.
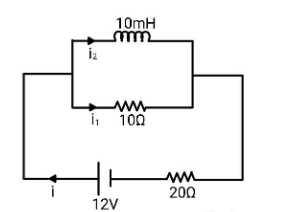
Solution
Here, you are given a circuit and the components of the circuit are 2 resistors, one inductor and a battery as a source of voltage. You are asked to find the current in the inductor when the current in the battery is 0.50A. What you need to do here is, consider the circuit as a combination of two circuits. One circuit will have branches containing resistors and the other circuit will have branches containing the inductor. Derive the equational form of current and accordingly find the value of the current in the inductor when the current from battery is 0.50A. Use Kirchhoff’s loop law.
Complete step by step answer:
Let us write the equations by applying the Kirchhoff’s loop law. First consider the loop containing the battery, 20Ω resistor and the 10Ω resistor. The equation will be given by
- \left( i \right)\left( {20} \right) + 12 - \left( {{i_1}} \right)\left( {10} \right) = 0 \\\
\Rightarrow 10i + 5{i_1} = 6 \\\
Now, let us consider the loop containing the battery, 20Ω resistor and the 10mH inductor. The corresponding equation will be given by
- \left( i \right)\left( {20} \right) + 12 - L\dfrac{{d{i_2}}}{{dt}} = 0 \\\
\Rightarrow 20i + L\dfrac{{d{i_2}}}{{dt}} = 12...\left( 2 \right) \\\
Let us write all the equations in terms of i and i2. We have i=i1+i2→i1=i−i2, we will substitute this value in our equations.
10i+5(i−i2)=6 ⇒15i−5i2=6...(1) ⇒i=156+5i2
Now, we also have i=156+5i2→i2=515i−6. Hence, we have i2 in terms of i.So, when i=0.5A, we have
i2=515(0.5)−6 ⇒i2=57.5−6 ⇒i2=51.5 ∴i2=0.3A.
Therefore, the current (in mA) in the ideal inductor when the current in the battery is 0.50A in the direction shown is 0.3A.
Note: The current in the circuit will be time dependent because we have an inductor in the circuit. The current as a function of time can be derived by obtaining i2 explicitly and then integrating the equation as per requirement. You should remember the potential difference that occurs across an inductor and also you should have a good idea of applying the Kirchhoff’s loop law perfectly.
