Question

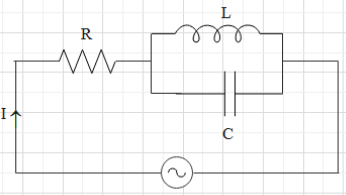
For the circuit shown in the Figure, the current through the inductor is 0.9 A while the current through the condenser is 0.4 A

A. Current drawn from generator $I=1.13A$
B. $\omega =\dfrac{1}{(1.5LC)}$
C. $I=0.5A$
D. $I=0.6A$

Answer 1

We are given an LCR circuit that consists of a resistor, capacitor and an inductor. The point to be noted here is that the current that passes through the inductor as well as the capacitor always maintains a phase difference of 180 degree. Substituting this property in the required formula, we can easily approach the solution to the given problem.

Complete answer:
In the question, we are given an LCR circuit where the inductor and the capacitor are connected in parallel and this circuit segment is connected in series to the resistor. It is also given that the current through the inductor is 0.9 A while the current through the condenser is 0.4 A.We know that the voltage across the circuit V can be found by the formula
$V={{V}_{0}}\sin \omega t$
From this, we can deduce that

The current through the capacitor is ${{I}_{c}}={{I}_{o}}\sin (\omega t-\dfrac{\pi }{2})$
And the current through the inductor is ${{I}_{L}}={{I}_{o}}\sin (\omega t+\dfrac{\pi }{2})$
This is so because the current values maintain a phase difference of 180 degrees.Hence, upon substituting values, the current from both the branches will be $0.9+(-0.4)=0.5A$

Thus we can conclude that option C is the correct answer.

Note: The nature of the circuit is dependent on the values of the inductive reactance and the capacitive reactance. When the inductive reactance exceeds, the circuit acts as an inductive circuit. If the capacitive resistance exceeds, it acts as a capacitive circuit. If both the values are zero, it acts as a resonant circuit.