Question

For the circuit shown in the figure,

This question has multiple correct options
A. the current I through the battery is 7.5mA
B. the potential difference across ${{R}_{L}}$ is 18V
C. ratio of power dissipated in ${{R}_{1}}$ and ${{R}_{2}}$ is 3
D. if ${{R}_{1}}$ and ${{R}_{2}}$ are interchanged, magnitude of the power dissipated in ${{R}_{L}}$ will decrease by a factor of 9

Answer 1

To solve this question, first obtain the equivalent resistance in the circuit. Then using the voltage, current and resistance relation we can find the current through the circuit. Now, find the voltage across the resistances and use the power, voltage and resistance relation to find the power dissipated through the resistances. With the resistances interchanged, follow the similar procedure to find the required answer.

Complete answer:
Consider the given figure in the question.
The given resistances are,
$\begin{aligned} & {{R}_{1}}=2k\Omega =2\times {{10}^{3}}\Omega \\\ & {{R}_{2}}=6k\Omega =6\times {{10}^{3}}\Omega \\\ & {{R}_{L}}=1.5k\Omega =1.5\times {{10}^{3}}\Omega \\\ \end{aligned}$
Now, to find the current through the battery, we need to find the equivalent resistance through which the current is passed.
The equivalent resistance of ${{R}_{2}}$ and ${{R}_{L}}$ is,
$\begin{aligned} & \dfrac{1}{{{R}'}}=\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{L}}} \\\ & \dfrac{1}{{{R}'}}=\dfrac{1}{6k\Omega }+\dfrac{1}{1.5k\Omega }=\dfrac{7.5}{6\times 1.5} \\\ & {R}'=\dfrac{6\times 1.5}{7.5} \\\ & {R}'=\dfrac{6}{5}k\Omega \\\ \end{aligned}$
The total resistance of the circuit will be,
$\begin{aligned} & R={{R}_{1}}+{R}' \\\ & R=2k\Omega +\dfrac{6}{5}k\Omega \\\ & R=3.2k\Omega \\\ \end{aligned}$
The voltage of the battery connected in the circuit is $V=24V$
Let, the current passing through the battery will be I.
So, the current through the battery will be,
$\begin{aligned} & I=\dfrac{V}{R} \\\ & I=\dfrac{24V}{3.2K} \\\ & I=7.5mA \\\ \end{aligned}$
The potential difference across the resistance ${{R}_{1}}$ is,
${{V}_{1}}=I\times {{R}_{1}}=7.5mA\times 2k\Omega =15V$
The potential difference across the resistance ${{R}_{1}}$ is,
${{V}_{2}}=24V-15V=9V$
So, the potential difference across the resistance ${{R}_{L}}$ will also be 9V.
Now, the ratio of the power dissipated in ${{R}_{1}}$ and ${{R}_{2}}$ is,
$\begin{aligned} & {{P}_{1}}:{{P}_{2}}=\dfrac{V_{1}^{2}}{{{R}_{1}}}:\dfrac{V_{2}^{2}}{{{R}_{2}}} \\\ & {{P}_{1}}:{{P}_{2}}=\dfrac{\dfrac{{{15}^{2}}}{2}}{\dfrac{{{9}^{2}}}{6}}=\dfrac{225}{2}\times \dfrac{6}{81} \\\ & {{P}_{1}}:{{P}_{2}}=\dfrac{25}{3} \\\ \end{aligned}$
In this configuration, the power dissipated through ${{R}_{{{L}_{{}}}}}$will be,
${{P}_{L}}=\dfrac{V_{2}^{2}}{{{R}_{L}}}=\dfrac{{{9}^{2}}}{1.5\times {{10}^{3}}}=54mW$
Now, interchanging the position of the resistances ${{R}_{1}}$ and ${{R}_{2}}$,

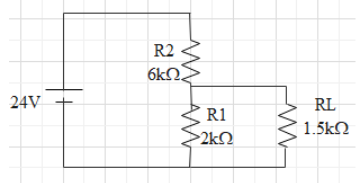
The equivalent resistances of ${{R}_{1}}$and ${{R}_{2}}$ will be,
${R}'=\dfrac{2\times 1.5}{2+1.5}=\dfrac{3}{3.5}$
Now, the voltage through ${{R}_{1}}$ or ${{R}_{L}}$ will be, ${{V}_{L}}=\dfrac{{{R}'}}{{{R}_{2}}+{R}'}\times 24V=\dfrac{\dfrac{3}{3.5}}{6+\dfrac{3}{3.5}}\times 24=3V$
So, the power dissipated through ${{R}_{L}}$ will be,
${{P}_{L}}^{\prime }=\dfrac{{{V}_{L}}^{2}}{{{R}_{L}}}=\dfrac{{{3}^{2}}}{1.5}=6mW$
The ratio of the power ${{P}_{L}}^{\prime }$ and ${{P}_{L}}$ will be,
$\dfrac{{{P}_{L}}^{\prime }}{{{P}_{L}}}=\dfrac{3mW}{54mW}=\dfrac{1}{9}$
After the resistances are interchanged, the power through the resistances are decreased by a factor of 9.

So, the correct options are (A) and (D).

Note:
As shown in the second part of the question, in the first part also we can directly find the potential differences across the resistances. In the first part we have found out the current because we are asked to find the current in the circuit.