Question

For the circuit shown in the figure, each of the resistance having resistance of 2 $\Omega$, then

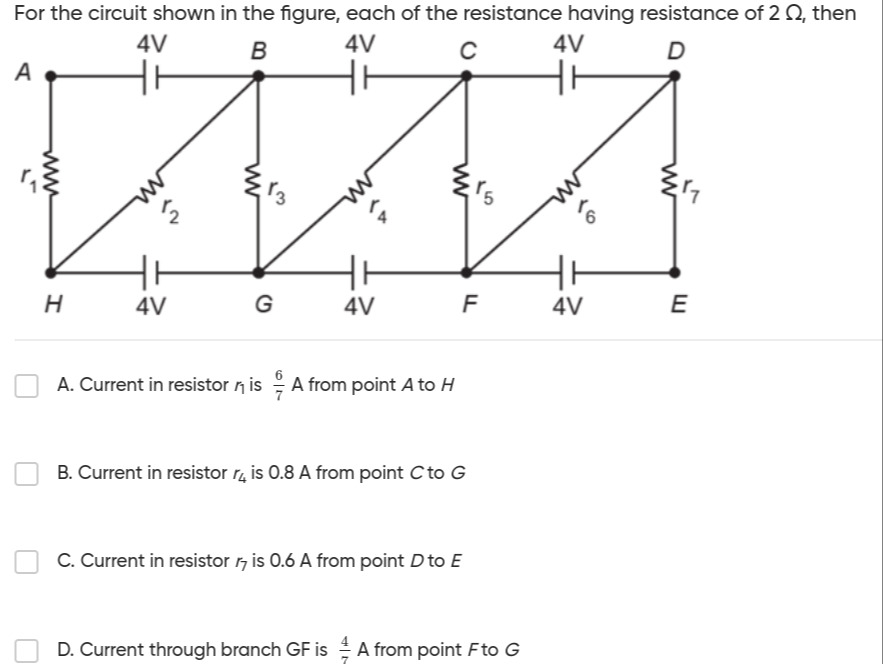
• A. Current in resistor $r_1$ is $\frac{6}{7}$ A from point $A$ to $H$
• B. Current in resistor $r_4$ is 0.8 A from point $C$ to $G$
• C. Current in resistor $r_7$ is 0.6 A from point $D$ to $E$
• D. Current through branch GF is $\frac{4}{7}$ A from point $F$ to $G$

Answer 1

None of the options are correct.

Answer 2

The circuit consists of resistors and voltage sources. All resistors have a resistance of $R = 2 \, \Omega$. All voltage sources have a voltage of $4 \, V$.

Assign potentials to the nodes. Choose an arbitrary reference point. Let the potential at node E be $0 \, V$.

From the bottom line, the batteries are connected in series such that the potential increases by $4 \, V$ when moving from right to left across each battery.

$V_E = 0 \, V$

$V_F = V_E + 4 \, V = 0 + 4 = 4 \, V$

$V_G = V_F + 4 \, V = 4 + 4 = 8 \, V$

$V_H = V_G + 4 \, V = 8 + 4 = 12 \, V$

So, the potentials of the bottom nodes are:

$V_E = 0 \, V$

$V_F = 4 \, V$

$V_G = 8 \, V$

$V_H = 12 \, V$

Now, consider the top line. The batteries are connected in series such that the potential increases by $4 \, V$ when moving from left to right across each battery.

Let $V_A$ be the potential at node A.

$V_B = V_A + 4 \, V$

$V_C = V_B + 4 \, V = V_A + 8 \, V$

$V_D = V_C + 4 \, V = V_A + 12 \, V$

We can use nodal analysis. Since nodes A, B, C, D are connected by ideal voltage sources, they form a supernode. The sum of currents leaving this supernode must be zero. The currents leaving the supernode are through the resistors connecting the top nodes to the bottom nodes.

Let's list the resistors and their connections correctly:

$r_1$: A to H

$r_2$: B to H

$r_3$: B to G

$r_4$: C to G

$r_5$: C to F

$r_6$: D to F

$r_7$: D to E

Sum of currents leaving the supernode (A, B, C, D):

$I_{AH} + I_{BH} + I_{BG} + I_{CG} + I_{CF} + I_{DF} + I_{DE} = 0$

$\frac{V_A - V_H}{R} + \frac{V_B - V_H}{R} + \frac{V_B - V_G}{R} + \frac{V_C - V_G}{R} + \frac{V_C - V_F}{R} + \frac{V_D - V_F}{R} + \frac{V_D - V_E}{R} = 0$

Multiply by $R$ (since all $R=2 \, \Omega$):

$(V_A - V_H) + (V_B - V_H) + (V_B - V_G) + (V_C - V_G) + (V_C - V_F) + (V_D - V_F) + (V_D - V_E) = 0$

Substitute the known potentials $V_H=12, V_G=8, V_F=4, V_E=0$:

$(V_A - 12) + (V_B - 12) + (V_B - 8) + (V_C - 8) + (V_C - 4) + (V_D - 4) + (V_D - 0) = 0$

Now substitute $V_B = V_A + 4$, $V_C = V_A + 8$, $V_D = V_A + 12$:

$(V_A - 12) + ((V_A+4) - 12) + ((V_A+4) - 8) + ((V_A+8) - 8) + ((V_A+8) - 4) + ((V_A+12) - 4) + ((V_A+12) - 0) = 0$

Simplify the terms:

$(V_A - 12) + (V_A - 8) + (V_A - 4) + (V_A) + (V_A + 4) + (V_A + 8) + (V_A + 12) = 0$

Combine $V_A$ terms: There are 7 terms of $V_A$.

$7V_A$

Combine constant terms:

$-12 - 8 - 4 + 0 + 4 + 8 + 12 = 0$

So, the equation becomes:

$7V_A + 0 = 0$

$V_A = 0 \, V$

Now we have all potentials:

$V_A = 0 \, V$

$V_B = V_A + 4 = 4 \, V$

$V_C = V_A + 8 = 8 \, V$

$V_D = V_A + 12 = 12 \, V$

$V_E = 0 \, V$

$V_F = 4 \, V$

$V_G = 8 \, V$

$V_H = 12 \, V$

Now let's check each option:

A. Current in resistor $r_1$ is $\frac{6}{7}$ A from point $A$ to $H$

$r_1$ is between A and H.

$I_{AH} = \frac{V_A - V_H}{R} = \frac{0 - 12}{2} = -6 \, A$.

The current from A to H is $-6 \, A$, which means $6 \, A$ from H to A.

So, statement A is incorrect.

B. Current in resistor $r_4$ is 0.8 A from point $C$ to $G$

$r_4$ is between C and G.

$I_{CG} = \frac{V_C - V_G}{R} = \frac{8 - 8}{2} = \frac{0}{2} = 0 \, A$.

So, statement B is incorrect.

C. Current in resistor $r_7$ is 0.6 A from point $D$ to $E$

$r_7$ is between D and E.

$I_{DE} = \frac{V_D - V_E}{R} = \frac{12 - 0}{2} = \frac{12}{2} = 6 \, A$.

So, statement C is incorrect.

D. Current through branch GF is $\frac{4}{7}$ A from point $F$ to $G$

Branch GF refers to the current flowing through the battery between F and G. The current from F to G through the battery is $12 \, A$.

So, statement D is incorrect.

Therefore, none of the options are correct.