Solveeit Logo
Login

Question

Question: For the circuit shown below let \[{I_1}\], \[{I_2}\] and \[{I_3}\] be the current marked in respecti...

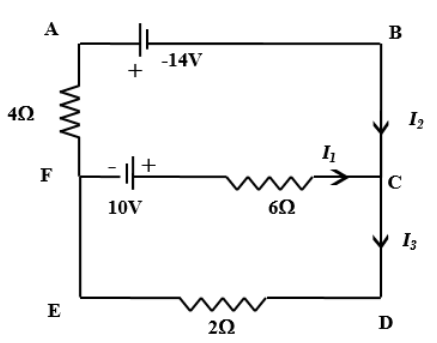
For the circuit shown below let I1{I_1}, I2{I_2} and I3{I_3} be the current marked in respective branches, then

A. I1=0.22A,I2=5.44A,I3=5.66A{I_1} = 0.22A,{I_2} = 5.44A,{I_3} = 5.66A
B. I1=−2A,I2=−3A,I3=−1A{I_1} = - 2A,{I_2} = - 3A,{I_3} = - 1A
C. I1=2A,I2=3A,I3=−1A{I_1} = 2A,{I_2} = 3A,{I_3} = - 1A
D. I1=−2A,I2=3A,I3=1A{I_1} = - 2A,{I_2} = 3A,{I_3} = 1A

Explanation

Solution

The given circuit represents an electrical network. There are three currents in the circuit, namelyI1{I_1}, I2{I_2} and I3{I_3}. The values of these currents can be found out by Kirchhoff’s Voltage Law or loop theorem. It states that, in a closed loop of an electrical network, the algebraic sum of the potential differences for all the components plus the algebraic sum of emfs is equal to zero.

Complete step by step answer:
The given circuit is a combination of various electric circuit elements (components) and sources of emf and voltages connected in a complicated manner. This is called an electrical network. The emf is positive if we traverse from the negative terminal to the positive terminal inside the cell and the emf is negative if we traverse from the positive terminal to the negative terminal.
In loop ABCFA,
14V+6I1−10V+4I3=014V + 6{I_1} - 10V + 4{I_3} = 0
This can be also written as
6I1+4I3=24V6{I_1} + 4{I_3} = 24V →(1) \to (1)
In loop FCDEF,
10V+6I1−2I3=010V + 6{I_1} - 2{I_3} = 0
This can be also written as
6I1−2I3=−10V6{I_1} - 2{I_3} = - 10V →(2) \to (2)
Subtracting equation (1) from equation (2)

\Rightarrow {I_3} = 5.66A$$ Substituting the value of $${I_3}$$ in equation (2) $$6{I_1} - 2\left( {5.66} \right) = - 10 \\\ \Rightarrow 6{I_1} = - 10 + 11.33 \\\ \Rightarrow 6{I_1} = 1.33 \\\ \Rightarrow {I_1} = 0.22A$$ Sum of currents flowing toward a junction is equal to the sum of currents flowing away from the junction. Therefore, at junction C $${I_2} + {I_1} = {I_3} \\\ \Rightarrow {I_2} = {I_3} - {I_1} \\\ \Rightarrow {I_2} = 5.66 - 0.22 \\\ \therefore {I_2} = 5.44A$$ The values of currents $${I_1}$$, $${I_2}$$ and $${I_3}$$ are $$0.22A$$, $$5.44A$$ and $$5.66A$$respectively. **Hence, option A is the correct answer.** **Note:** The Kirchhoff’s Voltage Law or loop theorem is only applicable for closed circuits. As the sun of all the potential differences and the emf’s is zero, the Kirchhoff’s Voltage Law is in accordance with the conservation of energy. In that closed loop of electrical network, if the direction of tracing is same as that of the conventional current flow then the potential difference across the resistances is considered as negative otherwise it is positive.