Solveeit Logo
Login

Question

Question: For the circles \({x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0\)and \({x^2} + {y^2} + 6x - 14y + 42 = ...

For the circles x2+y2−10x+16y+89−r2=0{x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0and x2+y2+6x−14y+42=0{x^2} + {y^2} + 6x - 14y + 42 = 0 which of the following is/are true.
(A) Number of integral values of r are 14 for which circles are intersecting.
(B) Number of integral values of r are 9 for which circles are intersecting.
(C) For r equal to 13, the number of common tangents is 3.
(D) For r equal to 21, the number of common tangents are 2.

Explanation

Solution

The equations of two circles are given. Find their radii and their centres. Next, check if the sum of their radii is greater/equal/less than the distance between their centres. Note that, if two circles intersect, then the sum of their radii must be greater than the distance between their centres. By using these conditions we will get the required solution.

Complete step by step Answer:

We know that the general equation of a circle is given by ax2+by2+2gx+2fy+c=0a{x^2} + b{y^2} + 2gx + 2fy + c = 0 ,

∴ Its centre is located at=(−g, −f) = ( - g,{\text{ }} - f)
And its radius is given by =g2+f2−c units = \sqrt {{g^2} + {f^2} - c} {\text{ units}}
Now, the equation of the first circle is given by x2+y2−10x+16y+89−r2=0{x^2} + {y^2} - 10x + 16y + 89 - {r^2} = 0
Therefore, its centre C1 is at (5,−8)(5, - 8)
And its radius r1 is given by
=(5)2+(−8)2−(89−r2)= \sqrt {{{(5)}^2} + {{\left( { - 8} \right)}^2} - \left( {89 - {r^2}} \right)}
On simplification we get,
=25+64−89+r2= \sqrt {25 + 64 - 89 + {r^2}}
On adding first two terms and on simplification we get,
=r= runits
Again, the equation of the second circle is given by x2+y2+6x−14y+42=0{x^2} + {y^2} + 6x - 14y + 42 = 0
Therefore, its centre C2 is at (−3, 7)( - 3,{\text{ }}7)
And its radius r2 is given by
=(−3)2+(7)2−42= \sqrt {{{\left( { - 3} \right)}^2} + {{\left( 7 \right)}^2} - 42}
On simplification we get,
=9+49−42= \sqrt {9 + 49 - 42}
On adding the terms we get,
=16= \sqrt {16}
On taking positive square root we get,
=4= 4 units
Now we know that the distance between the points (x1, y1) and (x2, y2) is given by
 =(x2−x1)2+(y2−y1)2{\text{ }} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}
Therefore the distance between the centres of the two circles is
C1C2=(5+3)2+(−8−7)2{C_1}{C_2} = \sqrt {{{\left( {5 + 3} \right)}^2} + {{\left( { - 8 - 7} \right)}^2}}
On simplification we get,
=64+225= \sqrt {64 + 225}
On adding we get,
=289= \sqrt {289}
On taking positive square root we get,
=17 = 17{\text{ }}units
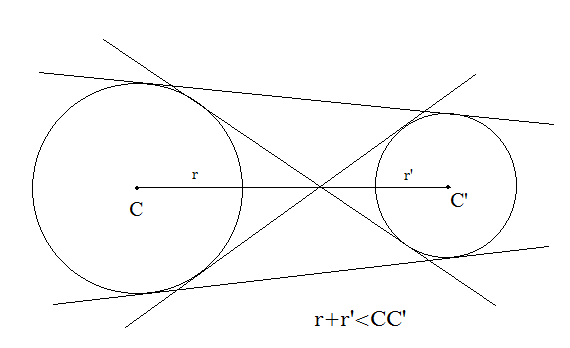
Now, if these two circles intersect, therefore the sum of their radii must be greater than the distance between their centres. In that case the number of common tangents will be 2.

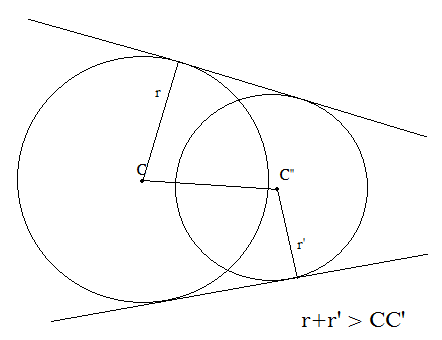
⇒r1+r2>17\Rightarrow {r_1} + {r_2} > 17
On substituting the values we get,
⇒r+4>17\Rightarrow r + 4 > 17
⇒r>13\Rightarrow r > 13
∴ For r equal to 21, the number of common tangents is 2.


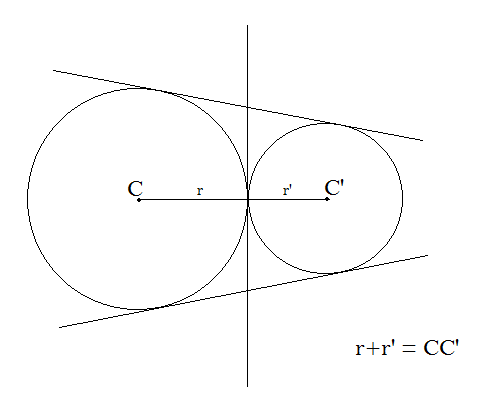
Again, the number of common tangents are 3 if and only if
r1+r2=17{r_1} + {r_2} = 17
On substituting the values we get,
⇒r+4=17\Rightarrow r + 4 = 17
⇒r=13\Rightarrow r = 13
∴ For r equal to 13, the number of common tangents is 3.
Therefore the correct options are (C) and (D).

Note: Note the 3 following cases:
Case 1: If two circles intersect, then the sum of their radii must be greater than the distance between their centres. In that case, the number of common tangents will be 2.

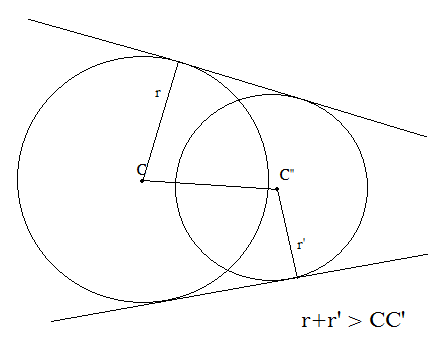
Case 2: If two circles meet at a single point, then the sum of their radii must be equal to the distance between their centres. In that case, the number of common tangents is 3.

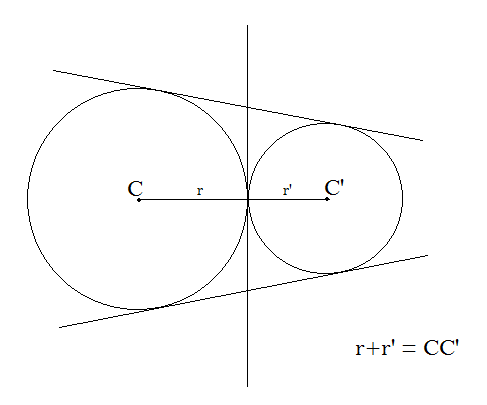
Case 3: If two circles neither meet nor intersect, then the sum of their radii must be less than the distance between their centres. In that case, the number of common tangents will be 4.