Question
Question: For the arrangement shown in the figure when the system is released, find the acceleration of the we...
For the arrangement shown in the figure when the system is released, find the acceleration of the wedge. Pulley and string are ideal and friction is absent.
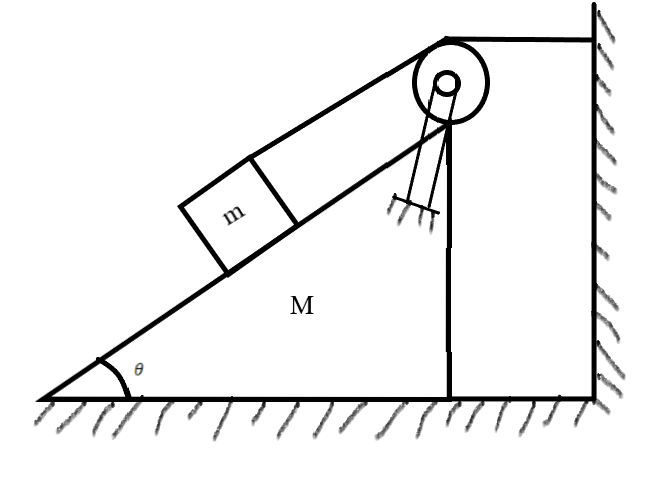
Solution
When the system is released, the block and wedge attached to the pulley start moving and their accelerations can be calculated by analyzing the forces acting on the block and the wedge from different directions. The forces acting on the block and the wedge can be studied by using Newton's second law of motion and drawing free body diagrams.
Complete step by step answer:
In the question, it is required to calculate the acceleration of the wedge, which can be found out from the various forces acting on the box and the wedge by drawing free body diagrams.
Let, the acceleration of the block be a1, and the acceleration of the wedge be a2. The tension in the string attached to the block is T, and the normal reaction on the block due to the wedge is N. When the system is released, the wedge tends to move towards the right and the block slips down. Since the length of the string does not change, so the displacement of the block and hence its acceleration will be equal to the acceleration of the wedge on the horizontal surface.
Therefore,
a1=a2=a
A free-body diagram of the forces acting on the block is shown in the figure below:
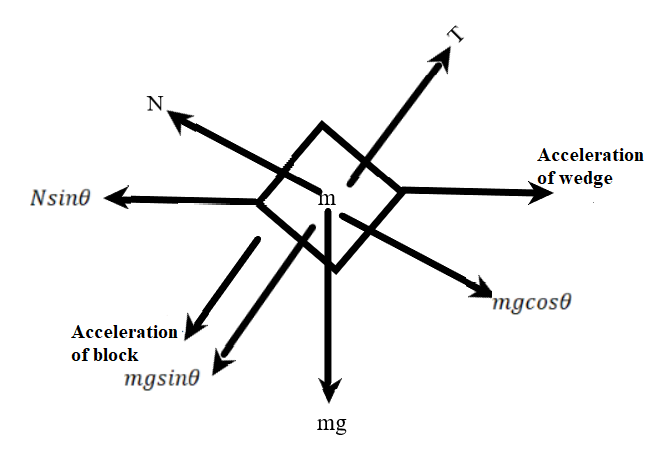
Now, balancing the forces acting on the block as
mgsinθ−T=ma1−ma2cosθ
⇒mgsinθ−T=ma−macosθ [From equation (1)]
⇒mgsinθ−T=ma(1−cosθ)
⇒−T=ma(1−cosθ)−mgsinθ
⇒T=mgsinθ−ma(1−cosθ) ...... (2)
Now, balancing the vertical forces as
mgcosθ−N=masinθ
⇒−N=masinθ−mgcosθ
⇒N=mgcosθ−masinθ ...... (3)
Now, balancing the forces acting in the wedge as
T−Tcosθ+Nsinθ=Ma
⇒T((1−cosθ)+Nsinθ=Ma ...... (4)
Substitute mgsinθ−ma(1−cosθ) for T, and mgcosθ−masinθ for Nin equation (4) as
[mgsinθ−ma(1−cosθ)]((1−cosθ)+[mgcosθ−masinθ]sinθ=Ma
⇒mgsinθ−mgsinθcosθ−ma(1−cosθ)2+mgsinθcosθ−masin2θ=Ma
⇒Ma=mgsinθ−ma(1−cosθ)2−masin2θ
⇒Ma+ma(1−cosθ)2+masin2θ=mgsinθ
⇒Ma+ma(1+cos2θ−2cosθ)+masin2θ=mgsinθ
⇒Ma+ma+macos2θ−2macosθ+masin2θ=mgsinθ
⇒Ma−2macosθ+ma(sin2θ+cos2θ)=mgsinθ
⇒Ma−2macosθ+ma=mgsinθ
⇒a(M−2mcosθ+m)=mgsinθ
⇒a=(M−2mcosθ+m)mgsinθ
Therefore the acceleration of the wedge is (M−2mcosθ+m)mgsinθ.
Note: Whenever the motion of a body on a plane surface or inclined surface needs to be studied, it is always useful to draw a free body diagram of the various forces on the body and the directions in which they act.
