Question

For $\text{Y}$ is inversely proportional to the square of $\text{X}$ when $\text{Y = 50, X = 2,}$ how do you find an equation connecting $\text{Y}$ and $\text{X}$?

Answer 1

It is given as $\text{A}$ is directly proportional to $\text{B}$. Then we can write this as $\text{A }\\!\\!\alpha\\!\\!\text{ B}$ and we can equate it by introducing a constant between $\text{A}$ and $\text{B}$ as $\text{A = KB}$ where $\text{K}$ is constant.
For finding the value of $\text{K}$ you need the values of $\text{A}$ and $\text{B}$ and then you can put it in equation to get the value of $\text{K}$.

Complete step by step solution: It is given in the question that $\text{Y}$ is inversely proportional to the square of $\text{X}$ we can write it as $\text{Y }\alpha \text{ }\dfrac{1}{{{x}^{2}}}$ and we can introduce constant $\text{C}$
$\therefore \text{Y = }\dfrac{\text{C}}{{{x}^{2}}}\,......\,(1)$
We have to find a equation connecting $\text{Y}$ and $\text{X}$ when $\text{Y = 50}$ and $\text{X = 2}$
So, the proportional equation becomes
$50\,=\,\dfrac{\text{C}}{{{\left( 2 \right)}^{2}}}$
$\text{C}\,\text{=}\,\text{50}\times {{2}^{2}}$
$\text{50}\times 4$
$\text{C}\,=\,200$
Putting the value of $\text{C}$ in equation $(1)$ we get,
$\text{Y}\,=\,\dfrac{200}{{{\text{X}}^{2}}}$, which could be written as ${{x}^{2}}y\,\,=\,200$
This is an equation connecting $\text{Y}$ and $\text{X}$ when $\text{Y = 50}$ and $\text{X = 2}$

Additional Information:
When $y$ is inversely proportional to the square of $x$. It means if $x$ is increased two times then, the value of $y$ decreases four times.
For example:
If $x\,=\,2$
$y\,=\,\dfrac{\text{C}}{{{x}^{2}}}\,=\,y\,=\,\dfrac{\text{C}}{{{2}^{2}}}\,=\,\dfrac{\text{C}}{4}$
The graph that represents this equation clearly.

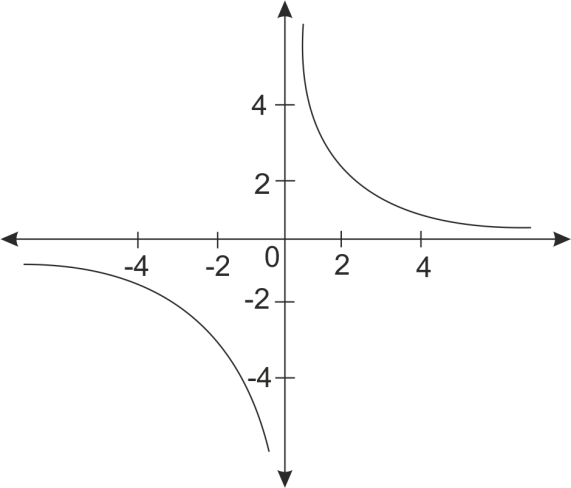
Let us discuss the case where $x$ is positive, if $x$ is positive, then
As $x\to \infty ,\,y\to 0$ and vice versa.
i.e if $x$ gets larger, $y$ gets smaller and vice versa.
Sometimes the question comes $y$ is inversely proportional to $x$ it can simply be written as $y\,=\,\dfrac{\text{C}}{x}\,$

Note:
When putting values of $y$ and $x$ in the given equation carefully solve and find the value of the constant you assumed.
It is not necessary to assume constant as $\text{C}$ you can assume any variable you wish.
The sign $\alpha$ is used for both inversely proportional and directly proportional questions.