Question

For some non-zero vector $\overrightarrow V$, if the sum of $\overrightarrow V$ and the vector obtained from $\overrightarrow V$ by rotating it by an angle $2\alpha$ equals to the vector obtained from $\overrightarrow V$ by rotating it by a then the value of $\alpha$, is where $n$ is a integer.
A.$2n\pi = \dfrac{\pi }{3}$
B.$n\pi = \dfrac{\pi }{3}$
C.$2n\pi = \dfrac{{2\pi }}{3}$
D.$n\pi = \dfrac{{2\pi }}{3}$

Answer 1

Hint : In this problem, A nonzero vector is a vector with magnitude not equal to zero. The vector obtained by rotating the vector $\overrightarrow V$ by an angle $\alpha$ in the anticlockwise direction is defined by trigonometric formula. A vector is an object that has both a magnitude and a direction.

Complete step-by-step answer :

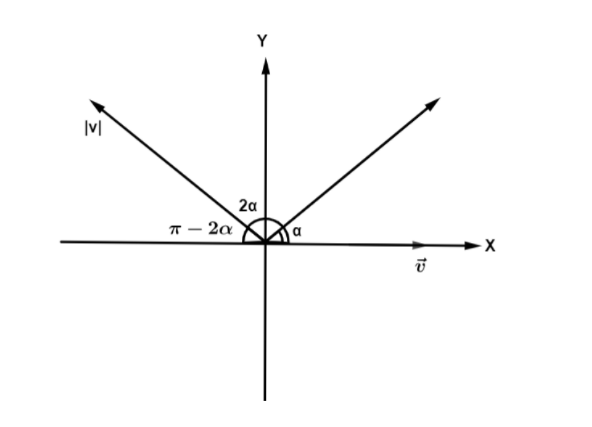
First, we have to sketch a diagram for some non-zero vector $\overrightarrow V$, if the sum of $\overrightarrow V$ and the vector obtained from $\overrightarrow V$ by rotating it by an angle $2\alpha$ equals to the vector obtained from $\overrightarrow V$ by rotating it by a then the value of $\alpha$, is where $n$ is a integer.
According to the condition in this problem, the vector obtained by rotating the vector $\overrightarrow V$ by an angle$\alpha$ in the anticlockwise direction, then
$vi - v\cos (\pi - 2\alpha )\hat i + v\sin (\pi - 2\alpha )\hat j = v\cos \alpha \hat i + v\sin \alpha \hat j$
We use the trigonometric identity $\cos (\pi - \theta ) = - \cos \theta$ and $\sin (\pi - \theta ) = \sin \theta$, we can get
Since, $\cos (\pi - 2\alpha ) = - \cos 2\alpha$ and $\sin (\pi - 2\alpha ) = \sin 2\alpha$
$v\hat i - v( - cos2\alpha \hat i) + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j$,
$v\hat i + vcos2\alpha \hat i + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j$
Put common factor ‘v’ from bracket, we have
$v(1 + cos2\alpha )\hat i + v\sin 2\alpha \hat j = v\cos \alpha \hat i + v\sin \alpha \hat j$
On separating i and j part on both sides of the equation, then
$v(1 + \cos 2\alpha ) = v\cos \alpha$ and $v\sin 2\alpha = v\sin \alpha$
By dividing on both sides by ‘v’, we get
$(1 + \cos 2\alpha ) = \cos \alpha$ and $\sin 2\alpha = \sin \alpha$
Here, by using this trigonometric identity , $\cos 2\alpha = 2{\cos ^2}\alpha - 1$ and $2\sin \alpha \cos \alpha = \sin \alpha$
$1 + 2{\cos ^2}\alpha - 1 = \cos \alpha$ and $2\sin \alpha \cos \alpha = \sin \alpha$
On further simplification, we get
$2{\cos ^2}\alpha = \cos \alpha$ and $2\cos \alpha = 1$
$2{\cos ^2}\alpha - \cos \alpha = 0$ and $\cos \alpha = \dfrac{1}{2}$
Take out $\cos \alpha$ commonly on the first function, then
$\cos \alpha (2\cos \alpha - 1) = 0$ and $\cos \alpha = \dfrac{1}{2}$
Separate the factors to find the value of , then
$\cos \alpha = 0$, $(2\cos \alpha - 1) = 0$ and $\cos \alpha = \dfrac{1}{2}$
Expanding the equation from LHS to RHS, then
$\cos \alpha = 0$, $2\cos \alpha = 1 \Rightarrow \cos \alpha = \dfrac{1}{2}$ and $\cos \alpha = \dfrac{1}{2}$
$\cos \alpha = 0$,$\cos \alpha = \dfrac{1}{2}$ and $\cos \alpha = \dfrac{1}{2}$
We know that, the formula $\cos \dfrac{\pi }{2} = 0 \Rightarrow \alpha = 2n\pi \pm \dfrac{\pi }{2}$ and $\cos \dfrac{\pi }{3} = \dfrac{1}{2} \Rightarrow \alpha = 2n\pi \pm \dfrac{\pi }{3}$,
$\alpha = 2n\pi \pm \dfrac{\pi }{2}$, $\alpha = 2n\pi \pm \dfrac{\pi }{3}$ and $\alpha = 2n\pi \pm \dfrac{\pi }{3}$
Therefore, $\alpha = 2n\pi \pm \dfrac{\pi }{3}$ satisfies both equations.
Hence, The final answer is option(A) $2n\pi = \dfrac{\pi }{3}$
So, the correct answer is “Option A”.

Note : Geometrically, we can define a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.