Question

For series LCR AC circuits shown in figure, the readings of and are the same ${V_2}$ and ${V_3}$ each equal to 100V. Then

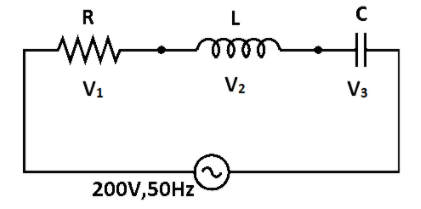
A) The reading ${V_1}$ is $200V$
B) The reading of ${V_2}$ is $0$
C) The circuit is in resonant mode
D) The inductive and capacitive reactance are equal.

Answer 1

Hint
For a series LCR circuit, the equation of voltage is given by $V = \sqrt {{V_1}^2 + {{({V_2} - {V_3})}^2}}$. Here, ${V_2}$ and ${V_3}$ are equal, so $V = \sqrt {{V_1}^2}$. Substitute the voltage of the cell and simplify to get the voltage across the resistor.

Complete step-by-step solution
The resistor, capacitor and the inductor are connected in series. For a series LRC circuit from the phasor diagram we know that,

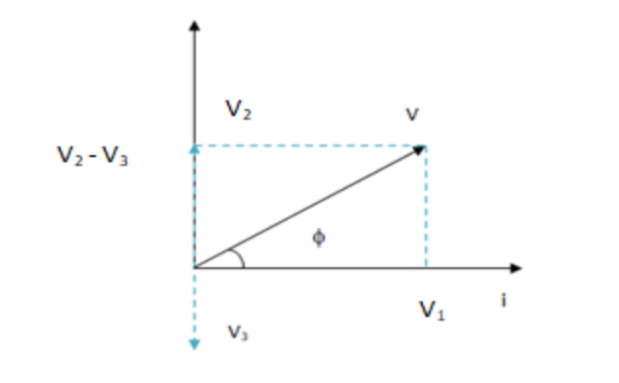
$V = \sqrt {{V_1}^2 + {{({V_2} - {V_3})}^2}}$
Where, ${V_1}$,${V_2}$ and ${V_3}$ are voltages of resistor, inductor and capacitor respectively.
Given in the question that,
${V_2} = {V_3} = 100V$
$V = 200V$
Substitute the voltage readings of capacitor and inductor in the equation of voltage.
$200 = \sqrt {{V_1}^2 + {{(100 - 100)}^2}}$
$200 = \sqrt {{V_1}^2 + 0}$
${V_1}^2 = {200^2}$
${V_1} = 100V$
Hence, the value of voltage across the resistor is ${V_1} = 100V$.
The correct option above is (A)

Note
For a series LCR circuit, Equation of current:
$i = {i_0}\sin (\omega t \pm \phi )$
Impedance of the circuit is given by:
$Z = \sqrt {{R^2} + {{({X_L} - {X_C})}^2}}$
Phase difference is given by:
$\tan \phi = \dfrac{{{V_L} - {V_C}}}{{{V_R}}}$
At resonance, the circuit behaves as a resistive circuit and the whole applied voltage appears across the resistance. The average power and the apparent power are equal at resonance. If the net reactance is inductive, the circuit behaves as an LR circuit. Similarly, when net reactance is capacitive then the circuit behaves as a CR circuit.