Question

For RLC parallel resonance circuit when $R=8k\Omega, L=80mH$and $C=0.50\mu F$; the Q factor is:
a) 10
b) 20
c) 40
d) 80

Answer 1

An RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC. It is shown below with the help of a diagram:

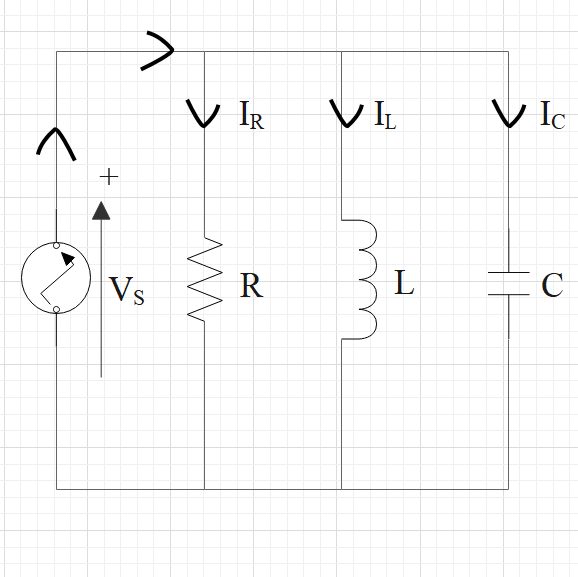
The selectivity or Q-factor for a parallel resonance circuit is the ratio of the circulating branch currents to the supply current, i.e.
$Q=R\sqrt{\dfrac{C}{L}}$
By using this formula, find the Q-factor for the given RLC parallel circuit.

Complete step by step answer:
As we have:
$\begin{aligned} & R=8k\Omega \\\ & L=80mH \\\ & C=0.50\mu F \\\ \end{aligned}$
So, by using the formula $Q=R\sqrt{\dfrac{C}{L}}$
We get:
$\begin{aligned} & Q=8\times {{10}^{3}}\Omega \sqrt{\dfrac{0.50\times {{10}^{-6}}F}{80\times {{10}^{-3}}H}} \\\ & =20 \end{aligned}$
So, we have Q-factor = 20

So, the correct answer is “Option B”.

Note:
The quality factor relates to the maximum or peak energy stored in the circuit (the reactance) to the energy dissipated (the resistance) during each cycle of oscillation. It is a dimensionless parameter. In parallel resonance RLC circuits, since the voltage remains the same across the circuit, so the quality factor gives the current magnification.
Similarly, for a series resonance RLC circuit, the current remains the same, so the quality factor gives the voltage magnification across the circuit.
Hence, we can say that the O- factor of a parallel resonance circuit is the inverse of the expression of the Q-factor of the series circuit.