Question

For resistance R and capacitance C in series, the impedance is twice that of a parallel combination of the same elements. What is the frequency of applied emf?

Answer 1

First analyse the AC series circuit. Find the impedance of this circuit by calculating the value of net voltage and net circuit. Similarly find the impedance of the second circuit. Then use the given data and find the value of the frequency of the source (applied emf).

Formula used:
${{V}_{R}}={{i}_{R}}R$
${{V}_{C}}=\dfrac{{{i}_{C}}}{2\pi fC}$
$Z=\dfrac{V}{i}$

Complete step by step answer:
The voltage across a resistance R in an AC circuit is given as ${{V}_{R}}={{i}_{R}}R$ …. (i),
where ${{i}_{R}}$ is the current flowing through the resistance.
The voltage across a capacitor with capacitance C in an AC circuit is given as ${{V}_{C}}=\dfrac{{{i}_{C}}}{2\pi fC}$…..(ii),
where ${{i}_{C}}$ is the current through the capacitor, f is the frequency of the applied alternating emf.
The impedance of an AC circuit is given as $Z=\dfrac{V}{i}$,
where V is the emf of the applied emf and the i is the net current in the circuit.
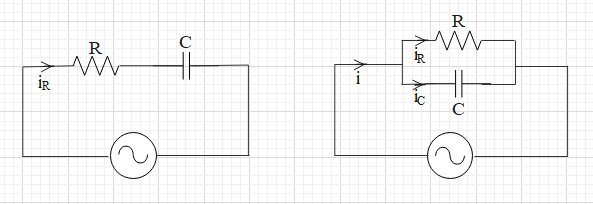
In the first figure, we see an AC circuit with resistance R and capacitance C in series connection. In this case, $i={{i}_{R}}={{i}_{C}}$ and $V=\sqrt{V_{R}^{2}+V_{C}^{2}}$.
Substitute the value of ${{V}_{R}}$ and ${{V}_{C}}$ from (i) and (ii).
$\Rightarrow V={{\left( {{i}_{R}}R \right)}^{2}}+{{\left( \dfrac{{{i}_{C}}}{2\pi fC} \right)}^{2}}$
$\Rightarrow V=\sqrt{\left( i_{R}^{2}{{R}^{2}} \right)+\left( \dfrac{i_{C}^{2}}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}} \right)}$
But $i={{i}_{R}}={{i}_{C}}$.
$\Rightarrow V=i\sqrt{\left( {{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}} \right)}$
$\Rightarrow \dfrac{V}{i}=\sqrt{\left( {{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}} \right)}$.
Let the impedance of this circuit be ${{Z}_{1}}$.
Therefore,
$\Rightarrow {{Z}_{1}}=\sqrt{\left( {{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}} \right)}$.
Now, let us find the impedance (${{Z}_{2}}$) of the second circuit.
In this AC circuit, the resistance R and capacitance C are connected in parallel. Therefore, $V={{V}_{R}}={{V}_{C}}$.
Substitute the value of ${{V}_{R}}$ and ${{V}_{C}}$ from (i) and (ii).
$\Rightarrow V={{i}_{R}}R=\dfrac{{{i}_{C}}}{2\pi fC}$.
This means that ${{i}_{R}}=\dfrac{V}{R}$ ….. (iii)
And ${{i}_{C}}=V(2\pi fC)$ ….. (iv).
Now, in this case the current through resistance and capacitance is 90 degrees. Therefore, the net current can be written as $i=\sqrt{i_{R}^{2}+i_{C}^{2}}$.
Substitute the values of ${{i}_{R}}$ and ${{i}_{C}}$ from (iii) and (iv).
$\Rightarrow i=\sqrt{{{\left( \dfrac{V}{R} \right)}^{2}}+{{\left( V(2\pi fC) \right)}^{2}}}$
$\Rightarrow i=V\sqrt{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}$
$\Rightarrow \dfrac{V}{i}=\dfrac{1}{\sqrt{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}}$
But, $\dfrac{V}{i}={{Z}_{2}}$
$\Rightarrow {{Z}_{2}}=\dfrac{1}{\sqrt{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}}$
From the given data we understand that ${{Z}_{1}}=2{{Z}_{2}}$.
$\Rightarrow \sqrt{{{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}C}}=\dfrac{2}{\sqrt{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}}$
$\Rightarrow \sqrt{{{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}C}}=\sqrt{\dfrac{4}{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}}$
$\Rightarrow {{R}^{2}}+\dfrac{1}{4{{\pi }^{2}}{{f}^{2}}C}=\dfrac{4}{\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)}$
.
$\Rightarrow \left( \dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}}+{{R}^{2}} \right)\left( \dfrac{1}{{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}} \right)=4$
Multiply the two brackets.
$\Rightarrow \dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}}+1+1+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}=4$
$\Rightarrow \dfrac{1}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}}+4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}=2$
Simplify further.
$\Rightarrow \dfrac{1+16{{\pi }^{4}}{{f}^{4}}{{C}^{4}}{{R}^{4}}}{4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}}=2$
$\Rightarrow 1+16{{\pi }^{4}}{{f}^{4}}{{C}^{4}}{{R}^{4}}=8{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}$
$\Rightarrow 16{{\pi }^{4}}{{f}^{4}}{{C}^{4}}{{R}^{4}}-8{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}+1=0$
$\Rightarrow {{\left( 4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}-1 \right)}^{2}}=0$
$\Rightarrow \left( 4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}-1 \right)=0$
$\Rightarrow 4{{\pi }^{2}}{{f}^{2}}{{C}^{2}}{{R}^{2}}=1$
$\Rightarrow {{f}^{2}}=\dfrac{1}{4{{\pi }^{2}}{{C}^{2}}{{R}^{2}}}$
Since f is always positive, $\Rightarrow f=\dfrac{1}{2\pi CR}$.
Therefore, the frequency of the applied emf is equal to $f=\dfrac{1}{2\pi CR}$.

Note:
The considered voltages and currents are mean values of the alternating voltages and currents.
Note that the voltages and the currents in an AC circuit cannot be added or subtracted algebraically because they are not always in phase.
Also note in the given figure an AC circuit with resistance R and capacitance C in series connection.