Question
Question: For positive integers n, p and q, define $I_n = \int_{0}^{\infty} \frac{1}{(e^x + e^{-x})^n} dx$...
For positive integers n, p and q, define
In=∫0∞(ex+e−x)n1dx
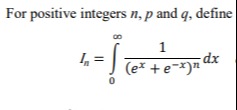
2n+1Γ((n+1)/2)πΓ(n/2)
Solution
The integral is given by In=∫0∞(ex+e−x)n1dx. We know that ex+e−x=2cosh(x). So, In=∫0∞(2cosh(x))n1dx=2n1∫0∞coshn(x)1dx=2n1∫0∞sechn(x)dx.
Let's evaluate the integral Jn=∫0∞sechn(x)dx. Use the substitution u=tanh(x). Then du=sech2(x)dx. Also, sech2(x)=1−tanh2(x)=1−u2. The limits of integration change from x=0 to u=tanh(0)=0 and from x→∞ to u=tanh(∞)=1. Jn=∫0∞sechn−2(x)sech2(x)dx=∫01(1−tanh2(x))(n−2)/2du=∫01(1−u2)(n−2)/2du.
Now, let's use the substitution u=sinθ. Then du=cosθdθ. The limits of integration change from u=0 to sinθ=0⟹θ=0 and from u=1 to sinθ=1⟹θ=π/2. The integral becomes: ∫0π/2(1−sin2θ)(n−2)/2cosθdθ=∫0π/2(cos2θ)(n−2)/2cosθdθ=∫0π/2cosn−2θcosθdθ=∫0π/2cosn−1θdθ.
This is a standard integral, a form of Wallis' integral. Let Km=∫0π/2cosmθdθ. Km={mm−1m−2m−3⋯212πmm−1m−2m−3⋯32if m is evenif m is odd. In our case, m=n−1.
So, Jn=∫0π/2cosn−1θdθ.
Case 1: n is even. Let n=2k for some positive integer k. Then m=n−1=2k−1 (odd). J2k=∫0π/2cos2k−1θdθ=2k−12k−22k−32k−4⋯32. This can be written using double factorials: J2k=(2k−1)!!(2k−2)!!. Then I2k=22k1J2k=22k1(2k−1)!!(2k−2)!!.
Case 2: n is odd. Let n=2k+1 for some non-negative integer k. Then m=n−1=2k (even). J2k+1=∫0π/2cos2kθdθ=2k2k−12k−22k−3⋯212π. This can be written using double factorials: J2k+1=(2k)!!(2k−1)!!2π=2kk!(2k−1)!!2π. Then I2k+1=22k+11J2k+1=22k+11(2k)!!(2k−1)!!2π=22k+12kk!(2k−1)!!2π=23k+1k!(2k−1)!!2π. A more common way to express this is using Gamma functions, which covers both even and odd cases. Jn=∫0π/2cosn−1θdθ. Using the relation between Wallis' integral and the Gamma function: ∫0π/2sinpxcosqxdx=2Γ(2p+q+2)Γ(2p+1)Γ(2q+1). Here, p=0 and q=n−1. Jn=2Γ(20+(n−1)+2)Γ(20+1)Γ(2(n−1)+1)=2Γ((n+1)/2)Γ(1/2)Γ(n/2). Since Γ(1/2)=π, Jn=2Γ((n+1)/2)πΓ(n/2).
Finally, In=2n1Jn=2n12Γ((n+1)/2)πΓ(n/2)=2n+1Γ((n+1)/2)πΓ(n/2).
This formula gives the value of In for any positive integer n.
