Question

For paraxial rays, show that the focal length of a spherical mirror is one-half of its radius of curvature.

Answer 1

A curved mirror is a mirror with the curved reflecting surfaces. If the inner side of the spherical mirror is reflecting then it is called a concave mirror and if the outer side of the spherical mirror is reflecting, it is called a convex mirror. To show that the focal length of a spherical mirror is one-half of its radius of curvature we can firstly make the ray diagram for both the mirrors and then apply congruence in triangles to reach the answer.

Complete step-by-step answer:
We will now prove the given formula for both the types of mirrors.
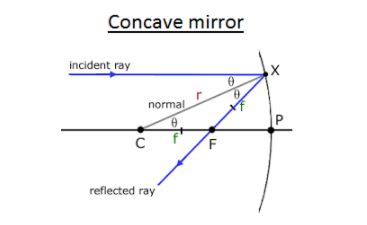
(a) Concave mirror
In the given figure P is the pole, F is the principal focus and C is the centre of curvature of a concave mirror of small aperture. Now, let us assume that a light ray AB be incident on the mirror in a direction parallel to the principal axis of the mirror. It gets reflected along BF. Join CB which is normal to mirror at B.
$\angle ABC=i$, angle of incidence
$\angle CBF=r$, angle of reflection
Now, $\angle ABC=\angle BCF=i$ (alternate angles)
In $\Delta CBF$ as i=r (law of reflection)
CF = FB
But as FB=FP because aperture is small
CF = FP
That is, F is the centre of PC
Hence, PF = $\dfrac{1}{2}$PC
Therefore, we get,
$f=\dfrac{R}{2}$

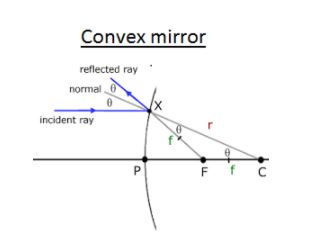
(b) Convex mirror
In the given figure P is the pole, F is the principal focus and C is the centre of curvature of a concave mirror of small aperture. Now, let us assume that a light ray AB be incident on the mirror in a direction parallel to the principal axis of the mirror. It gets reflected along BD and on producing back we see that it appears to come from principal focus F of the mirror. Join CB and produce it to N which is normal to mirror at B.
$\angle ABN=i$, angle of incidence
$\angle DBN=r$, angle of reflection
Now, $\angle FBC=\angle DBN=r$ (opposite angles)
$\angle BCF=\angle NBA=i$ (corresponding angles)
In $\Delta CBF$ as i=r (law of reflection)
CF = FB
But as FB=FP because aperture is small
CF = FP
That is, F is the centre of PC
Hence, PF = $\dfrac{1}{2}$PC
Therefore, we get,
$f=\dfrac{R}{2}$

Note: The paraxial approximation which we have used in this derivation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system. A paraxial ray is a ray which makes a small angle to the optical axis of the system and thus always lies close to the axis throughout the system.