Question
Question: For $p, n \in N$, let $f(x) = 1-x^p$ and $g_n(x) = \frac{n}{\frac{1}{f(x)}+\frac{1}{f(2x)}+....+\fra...
For p,n∈N, let f(x)=1−xp and gn(x)=f(x)1+f(2x)1+....+f(nx)1n. Find the value of limx→0xp1−gn(x) at n=5 and p=3.
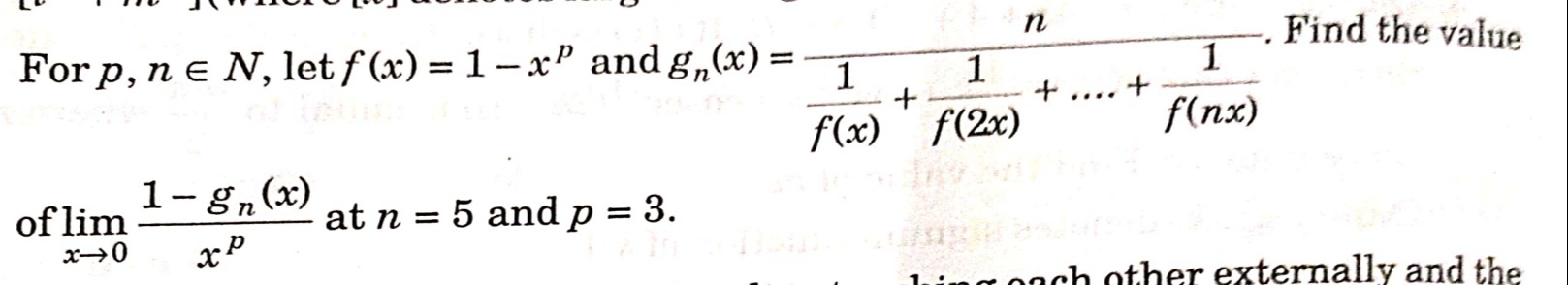
45
Solution
To find the value of the limit limx→0xp1−gn(x), where f(x)=1−xp and gn(x)=f(x)1+f(2x)1+....+f(nx)1n, we will use the Taylor series expansion.
First, let's express gn(x) in terms of f(kx): gn(x)=∑k=1nf(kx)1n
Substitute f(kx)=1−(kx)p=1−kpxp: gn(x)=∑k=1n1−kpxp1n
We know the geometric series expansion for 1−y1 for small y: 1−y1=1+y+y2+O(y3)
In our case, y=kpxp. As x→0, kpxp→0. So, we can write: 1−kpxp1=1+kpxp+(kpxp)2+O(x3p)=1+kpxp+k2px2p+O(x3p)
Let D(x) be the denominator of gn(x): D(x)=∑k=1n1−kpxp1=∑k=1n(1+kpxp+k2px2p+O(x3p)) D(x)=∑k=1n1+xp∑k=1nkp+x2p∑k=1nk2p+O(x3p)∑k=1n1 Let S1=∑k=1nkp and S2=∑k=1nk2p. D(x)=n+S1xp+S2x2p+O(x3p)
Now, substitute D(x) back into gn(x): gn(x)=n+S1xp+S2x2p+O(x3p)n
Next, we calculate 1−gn(x): 1−gn(x)=1−n+S1xp+S2x2p+O(x3p)n 1−gn(x)=n+S1xp+S2x2p+O(x3p)(n+S1xp+S2x2p+O(x3p))−n 1−gn(x)=n+S1xp+S2x2p+O(x3p)S1xp+S2x2p+O(x3p)
Finally, we find the limit: limx→0xp1−gn(x)=limx→0xpn+S1xp+S2x2p+O(x3p)S1xp+S2x2p+O(x3p) Divide the numerator by xp: limx→0n+S1xp+S2x2p+O(x3p)S1+S2xp+O(x2p)
As x→0, all terms containing x will go to zero. So, the limit simplifies to: nS1=n∑k=1nkp
Now, we apply the given values n=5 and p=3: The limit value is 5∑k=15k3.
Calculate the sum ∑k=15k3: ∑k=15k3=13+23+33+43+53 =1+8+27+64+125 =225
Substitute this sum back into the limit expression: Limit =5225=45.
The final answer is 45.
Explanation: The problem involves evaluating a limit of a function gn(x) which is defined in terms of a sum. The key insight is to use the Taylor series expansion for 1−y1=1+y+y2+... for small y. By substituting y=kpxp for each term in the sum, we can express the denominator of gn(x) as n+xp∑k=1nkp+O(x2p). Then, 1−gn(x) simplifies to n+O(xp)xp∑k=1nkp+O(x2p). Dividing by xp and taking the limit as x→0 yields n∑k=1nkp. Finally, substituting n=5 and p=3, we calculate the sum of the first five cubes and divide by 5, which gives 45.
