Question

For one mole of and ideal gas, the slope of $V$vs $T$ curve at constant pressure of $2atm$ is $X{\text{ }}Lmo{l^{ - 1}}{K^{ - 1}}$. The value of the ideal universal gas constant $'R'$ in terms of $X$ is:
A. $X{\text{ }}L{\text{ }}atm{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$
B. $\dfrac{X}{2}{\text{ }}L{\text{ }}atm{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$
C. $2X{\text{ }}L{\text{ }}atm{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$
D. $2X{\text{ }}atm{\text{ }}{L^{ - 1}}{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$

Answer 1

The gas constant (universal gas constant) is denoted by symbol $R$. It is equal to Boltzmann constant, but expressed in units of energy per temperature increment per mole i.e. the pressure- volume product, rather than energy per temperature, increment per particle.

Formula used: The ideal gas equation $\Rightarrow PV = nRT$

Complete step by step answer: The gas constant occurs in the ideal gas law as follows:
$PV = nRT = mRspecificT$
Where, $P$ is absolute pressure (SI units pascals), $V$ is volume of the gas (SI unit cubic metre), $n$ is the amount of gas (SI unit moles), $m$ is mass (SI unit kilograms) contained in $V$ and $T$ is the thermodynamic temperature (SI unit Kelvins), $R$ specific is the mass specific gas constant. The gas constant is expressed in the same physical units as molar entropy and molar heat capacity.
$R$specific $= \dfrac{R}{M} = Cp = Cv$
$M$= molar mass of gas mixture
$PV = nRT,{\text{ }}or,P\left( {\dfrac{v}{n}} \right) = RT$
Or $PVm = RT$
$\left( {Vm = molar{\text{ }}volume} \right)$
$Vm = \dfrac{R}{P}T$ ………. (i)
At constant pressure for $1$ mol of an ideal gas, $V = \dfrac{R}{P}T$
The relation represents a straight line passing through the equation, so, for $1$ mol of an ideal gas at constant pressure, the graph of $Vm$ vs $T$, will be a straight line with slope $R/P$.

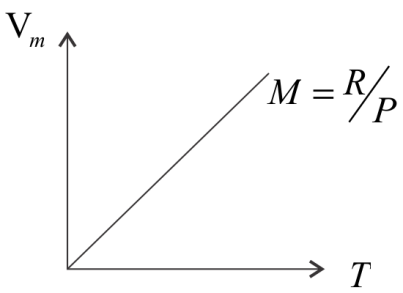
It is given in the equation that $\dfrac{R}{P} = m = X$=given
$\dfrac{R}{P} = X$
$\dfrac{R}{{2atm}} = X{\text{ }}L{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$
$R = 2X{\text{ }}L{\text{ }}atm{\text{ }}mo{l^{ - 1}}{K^{ - 1}}$.
So, the correct answer is “Option C”.

Note: The $R$ is known as gas constant or universal gas constant or ideal gas constant. It’s value is equal to approx. $8.31446261815324J{\text{ }}{K^{ - 1}}mo{l^{ - 1}}$.