Question
Question: For non-zero vectors $\bar{a}, \bar{b}, \bar{c}$ $|(\bar{a} \times \bar{b}).\bar{c}| = |\bar{a}| |\b...
For non-zero vectors aˉ,bˉ,cˉ ∣(aˉ×bˉ).cˉ∣=∣aˉ∣∣bˉ∣∣cˉ∣ holds iff.:
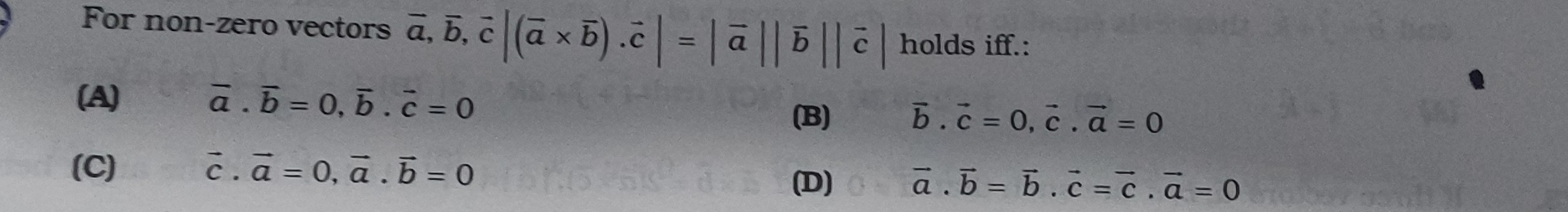
aˉ.bˉ=0,bˉ.cˉ=0
bˉ.cˉ=0,cˉ.aˉ=0
cˉ.aˉ=0,aˉ.bˉ=0
aˉ.bˉ=bˉ.cˉ=cˉ.aˉ=0
aˉ.bˉ=bˉ.cˉ=cˉ.aˉ=0
Solution
The given condition is ∣(aˉ×bˉ).cˉ∣=∣aˉ∣∣bˉ∣∣cˉ∣.
Let θ be the angle between vectors aˉ and bˉ (0≤θ≤π). The magnitude of the cross product is ∣aˉ×bˉ∣=∣aˉ∣∣bˉ∣sinθ.
Let nˉ=aˉ×bˉ. The vector nˉ is perpendicular to both aˉ and bˉ. Let ϕ be the angle between nˉ and cˉ (0≤ϕ≤π). The scalar triple product is (aˉ×bˉ).cˉ=nˉ.cˉ=∣nˉ∣∣cˉ∣cosϕ.
Substituting these into the given condition: ∣∣aˉ∣∣bˉ∣sinθ∣cˉ∣cosϕ∣=∣aˉ∣∣bˉ∣∣cˉ∣ ∣aˉ∣∣bˉ∣∣sinθ∣∣cˉ∣∣cosϕ∣=∣aˉ∣∣bˉ∣∣cˉ∣
Since aˉ,bˉ,cˉ are non-zero vectors, their magnitudes ∣aˉ∣,∣bˉ∣,∣cˉ∣ are positive. Also, since 0≤θ≤π, sinθ≥0, so ∣sinθ∣=sinθ. Thus, the equation becomes: ∣aˉ∣∣bˉ∣sinθ∣cˉ∣∣cosϕ∣=∣aˉ∣∣bˉ∣∣cˉ∣
We can divide both sides by ∣aˉ∣∣bˉ∣∣cˉ∣ (since they are non-zero): sinθ∣cosϕ∣=1
We know that:
- 0≤sinθ≤1 (for 0≤θ≤π)
- 0≤∣cosϕ∣≤1 (for 0≤ϕ≤π)
For the product of two numbers, both less than or equal to 1, to be equal to 1, both numbers must be equal to 1. Therefore, we must have:
- sinθ=1
- ∣cosϕ∣=1
Let's analyze these two conditions:
-
sinθ=1: This implies θ=2π (or 90∘). Since θ is the angle between aˉ and bˉ, this means aˉ is perpendicular to bˉ. So, aˉ.bˉ=0.
-
∣cosϕ∣=1: This implies cosϕ=1 or cosϕ=−1. This means ϕ=0 or ϕ=π. Since ϕ is the angle between nˉ=aˉ×bˉ and cˉ, this means cˉ is parallel to nˉ (or anti-parallel). As nˉ=aˉ×bˉ is a vector perpendicular to both aˉ and bˉ, if cˉ is parallel to nˉ, then cˉ must also be perpendicular to both aˉ and bˉ. So, cˉ⊥aˉ⟹cˉ.aˉ=0. And cˉ⊥bˉ⟹cˉ.bˉ=0.
Combining all conditions, for ∣(aˉ×bˉ).cˉ∣=∣aˉ∣∣bˉ∣∣cˉ∣ to hold, we must have: aˉ.bˉ=0 bˉ.cˉ=0 cˉ.aˉ=0
This means that the three vectors aˉ,bˉ,cˉ must be mutually orthogonal (perpendicular to each other).
