Question
Question: For non-negative integers s and r, let $\binom{s}{r} = \begin{cases} \frac{s!}{r!(s-r)!} & \text{if ...
For non-negative integers s and r, let (rs)={r!(s−r)!s!0if r≤sif r>s
For non-negative integers n and k, let Sn=∑k=0n(kn)k+12k+1
If e denotes the base of the natural logarithm, then which of the following is/are TRUE?
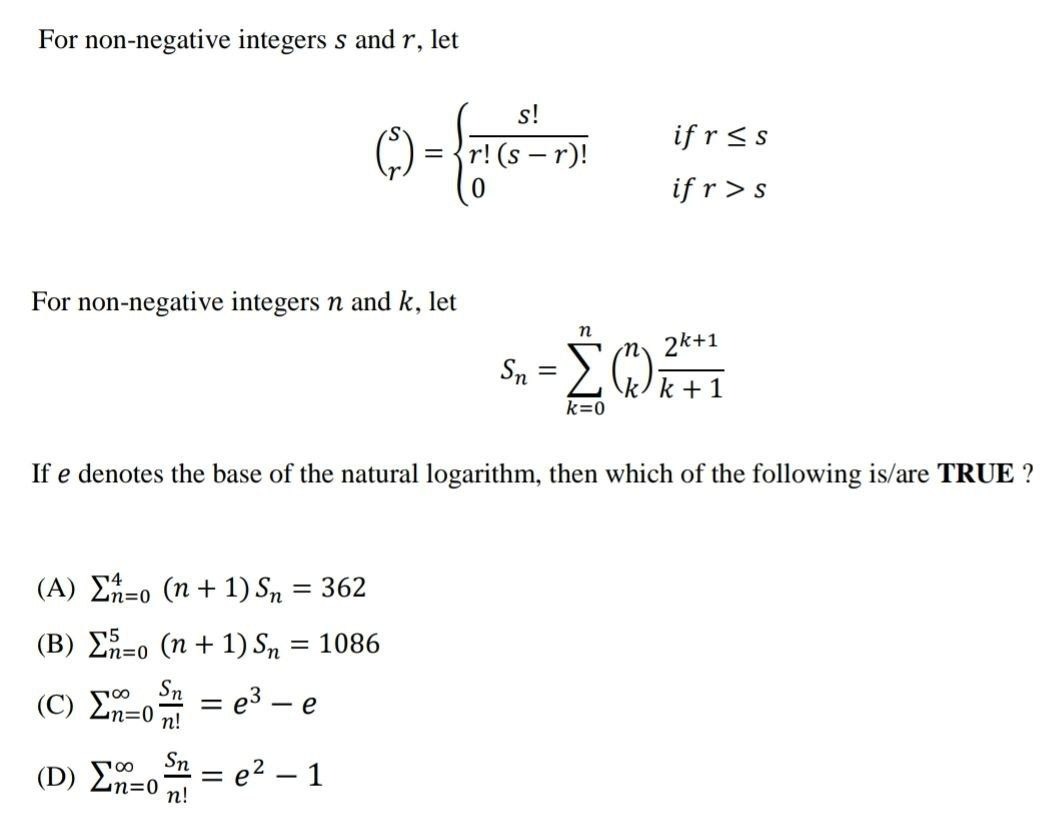
∑n=04(n+1)Sn=362
∑n=05(n+1)Sn=1086
∑n=0∞n!Sn=e3−e
∑n=0∞n!Sn=e2−1
(B), (C)
Solution
-
Simplify Sn: Sn=∑k=0n(kn)k+12k+1 Using k+11(kn)=n+11(k+1n+1): Sn=∑k=0nn+11(k+1n+1)2k+1=n+11∑k=0n(k+1n+1)2k+1 Let j=k+1: Sn=n+11∑j=1n+1(jn+1)2j From the binomial expansion (1+2)n+1=∑j=0n+1(jn+1)2j=3n+1: 3n+1=(0n+1)20+∑j=1n+1(jn+1)2j=1+∑j=1n+1(jn+1)2j So, ∑j=1n+1(jn+1)2j=3n+1−1. Therefore, Sn=n+11(3n+1−1).
-
Evaluate statements (A) and (B): (n+1)Sn=3n+1−1. (A) ∑n=04(n+1)Sn=∑n=04(3n+1−1)=(31−1)+(32−1)+(33−1)+(34−1)+(35−1) =(3+9+27+81+243)−5=363−5=358. Statement (A) is FALSE.
(B) ∑n=05(n+1)Sn=∑n=04(n+1)Sn+(5+1)S5=358+(35+1−1)=358+(36−1)=358+(729−1)=358+728=1086. Statement (B) is TRUE.
- Evaluate statements (C) and (D): n!Sn=(n+1)!3n+1−1. ∑n=0∞n!Sn=∑n=0∞(n+1)!3n+1−1. Let m=n+1. The sum becomes ∑m=1∞m!3m−1=∑m=1∞m!3m−∑m=1∞m!1. Using the Maclaurin series for ex=∑m=0∞m!xm=1+∑m=1∞m!xm, so ∑m=1∞m!xm=ex−1. ∑m=1∞m!3m=e3−1. ∑m=1∞m!1=e1−1=e−1. The total sum is (e3−1)−(e−1)=e3−e.
(C) ∑n=0∞n!Sn=e3−e. Statement (C) is TRUE. (D) ∑n=0∞n!Sn=e2−1. Statement (D) is FALSE because e3−e=e2−1.
The TRUE statements are (B) and (C).
