Question

For Mn$^{3+}$ ion, the electron pairing energy P is 28000 cm$^{-1}$, $\Delta_o$ values for the complexes [Mna$_6$]$^{3+}$ and [Mnb$_6$]$^{3-}$ are 21000 cm$^{-1}$ and 38500 cm$^{-1}$ respectively. If difference in number of t$_{2g}$ and e$_g$ electrons in [Mna$_6$]$^{3+}$ is 'x' and difference in number of t$_{2g}$ and e$_g$ electrons in [Mnb$_6$]$^{3-}$ is y then 10(2x + 3y) is ____

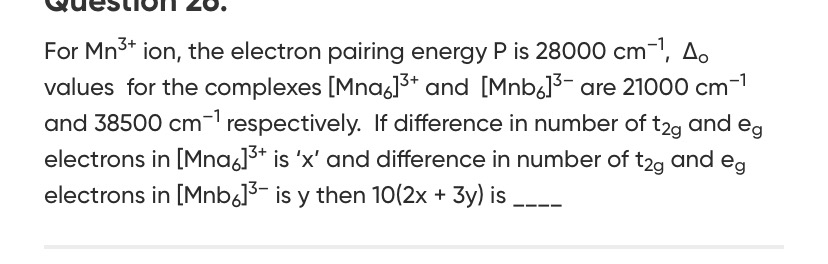
Answer 1

160

Answer 2

1. Determine the electronic configuration of Mn$^{3+}$: Manganese (Mn) has atomic number 25, with electronic configuration $[Ar] 3d^5 4s^2$. Thus, Mn$^{3+}$ has an electronic configuration of $3d^4$.

2. Analyze [Mna$_6$]$^{3+}$:

   • Given $\Delta_o = 21000 \text{ cm}^{-1}$ and pairing energy $P = 28000 \text{ cm}^{-1}$.
   • Since $\Delta_o < P$, the ligand 'a' is a weak field ligand, and the complex is high spin.
   • For a $d^4$ ion in an octahedral field, the high spin configuration is $t_{2g}^3 e_g^1$.
   • The number of $t_{2g}$ electrons is 3, and the number of $e_g$ electrons is 1.
   • 'x' is the difference in the number of $t_{2g}$ and $e_g$ electrons: $x = n_{t_{2g}} - n_{e_g} = 3 - 1 = 2$.

3. Analyze [Mnb$_6$]$^{3-}$:

   • Given $\Delta_o = 38500 \text{ cm}^{-1}$ and pairing energy $P = 28000 \text{ cm}^{-1}$.
   • Since $\Delta_o > P$, the ligand 'b' is a strong field ligand, and the complex is low spin.
   • For a $d^4$ ion in an octahedral field, the low spin configuration is $t_{2g}^4 e_g^0$.
   • The number of $t_{2g}$ electrons is 4, and the number of $e_g$ electrons is 0.
   • 'y' is the difference in the number of $t_{2g}$ and $e_g$ electrons: $y = n_{t_{2g}} - n_{e_g} = 4 - 0 = 4$.

4. Calculate the final expression:

   • Substitute the values of x and y into the expression $10(2x + 3y)$:
   • $10(2 \times 2 + 3 \times 4) = 10(4 + 12) = 10(16) = 160$.