Question

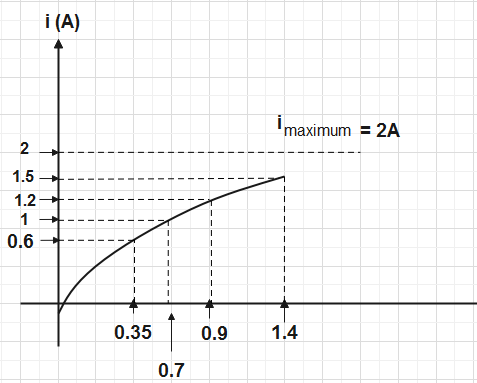
For L-R circuits, growth of current as a function of time $t$ is shown in the graph. Which of the following options represents the value of time constant most closely for the circuit?
(A). $0.7s$
(B). $1s$
(C). $2.4s$
(D). $0.4s$

Answer 1

The graph represents the relation between current and time interval. As the switch is turned on, a huge current flows through the circuit due to which the inductance comes into play. When the time interval is equal to the time constant, the value of current is equal to sixty seven percent of the maximum current. The time interval corresponding to this value of current is the time constant.

Formula used:
$\tau =\dfrac{L}{R}$

Complete step by step solution:
In an L-R circuit, when the switch is turned on, a huge current flows through the circuit. As the value of current changes with time, an opposite current flows through the circuit due to self inductance.
The time constant of a circuit is the ratio of the inductance to the resistance in a circuit. Therefore,
$\tau =\dfrac{L}{R}$
Here, $\tau$ is the time constant
$L$ is the inductance
$R$ is the resistance
When the time interval is equal to the time constant or $t=\tau$, the value of the current is $63$ of the maximum current.

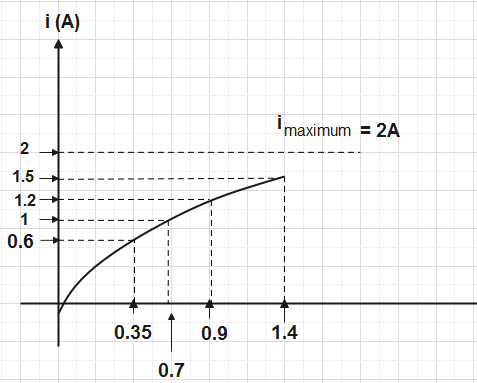
According to the graph, the maximum value of the current is $2A$. Let the value of current at time constant be $i$, then
$\begin{aligned} & i=0.63\times 2 \\\ & \Rightarrow i=1.26A \\\ \end{aligned}$
Current $1.2A$ corresponds to $0.9s$, so we can say that current $1.26A$ corresponds to approximately $1s$ on the graph.
Therefore, the option which represents the time constant for the circuit most accurately is $1s$.
Hence, the correct option is (B).

Note: The unit of time according to the definition of time constant is $H{{\Omega }^{-1}}$ or seconds. It is assumed that a circuit reaches its steady state at t= infinity. At steady state, the current in the circuit becomes constant. The reactance of an L-R circuit is equal to the sum of squares of resistance and reactance.