Question

For incident ray parallel to principle axis of one convex lens emerges parallel rays from other convex lens, if focal length of each lens is of magnitude is $f$ and separation between convex lenses is D and between left convex and concave is x.

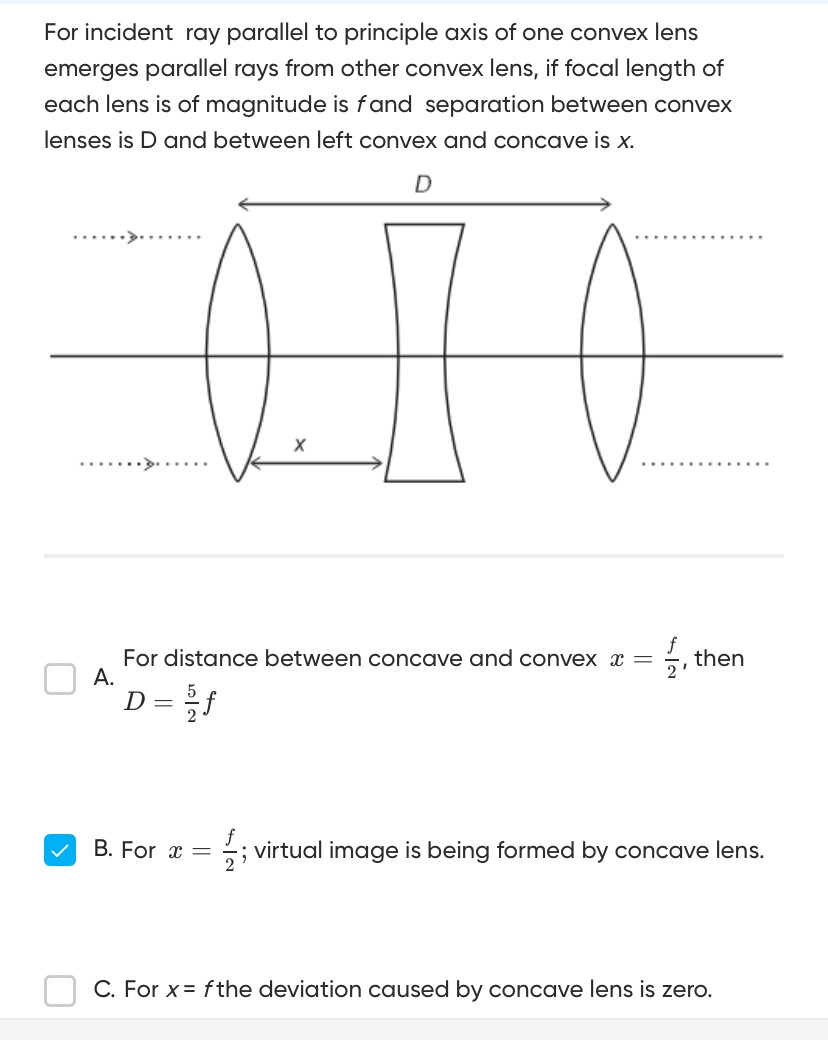
• A. For distance between concave and convex $x = \frac{f}{2}$, then $D = \frac{5}{2}f$
• B. For $x = \frac{f}{2}$; virtual image is being formed by concave lens.
• C. For $x = f$ the deviation caused by concave lens is zero.

Answer 1

Answer: (B)

A, C

Answer 2

The problem describes an optical system consisting of three lenses: a convex lens (Lens 1), a concave lens, and another convex lens (Lens 2). We are given information about the incident and emergent rays, and the focal lengths of the lenses. We need to evaluate the given statements.

Given:

• Focal length of each convex lens: $f_1 = +f$, $f_2 = +f$.
• Magnitude of focal length of concave lens: $f$. So, $f_c = -f$.
• Incident rays on Lens 1 are parallel to the principal axis.
• Emergent rays from Lens 2 are parallel to the principal axis.
• Separation between Lens 1 and concave lens is $x$.
• Separation between Lens 1 and Lens 2 is $D$.

Step-by-step Ray Tracing and Calculations:

1. Rays through Lens 1 (Convex):

   • Since incident rays are parallel to the principal axis, they converge at the focal point of Lens 1.
   • Image $I_1$ is formed at $v_1 = +f$ (to the right of Lens 1).

2. Rays through Concave Lens:

   • The image $I_1$ acts as the object for the concave lens.
   • The concave lens is at a distance $x$ from Lens 1.
   • The position of $I_1$ relative to the concave lens is $u_c = (f - x)$.
   • We assume $f > x$, meaning $I_1$ is to the right of the concave lens. This makes $I_1$ a virtual object for the concave lens, so $u_c = +(f-x)$.
   • Using the lens formula for the concave lens: $\frac{1}{v_c} - \frac{1}{u_c} = \frac{1}{f_c}$ $\frac{1}{v_c} - \frac{1}{+(f-x)} = \frac{1}{-f}$ $\frac{1}{v_c} = \frac{1}{f-x} - \frac{1}{f} = \frac{f - (f-x)}{f(f-x)} = \frac{x}{f(f-x)}$ So, $v_c = \frac{f(f-x)}{x}$.
   • Since $f>x$ and $f,x$ are positive, $v_c$ will be positive. A positive image distance ($v_c > 0$) indicates a real image formed to the right of the concave lens.

3. Rays through Lens 2 (Convex):

   • The emergent rays from Lens 2 are parallel to the principal axis. This implies that the object for Lens 2 must be at its principal focus.
   • So, the image $I_c$ (formed by the concave lens) must be located at $u_2 = -f_2 = -f$ (i.e., at a distance $f$ to the left of Lens 2).
   • The distance between the concave lens and Lens 2 is $(D-x)$.
   • Therefore, the position of $I_c$ from the concave lens ($v_c$) must be $(D-x) - f$. This implies $I_c$ is formed to the right of the concave lens and to the left of Lens 2.
   • Equating the two expressions for $v_c$: $\frac{f(f-x)}{x} = (D-x) - f$ $\frac{f^2 - fx}{x} = D-x-f$ $D = \frac{f^2 - fx}{x} + x + f$ $D = \frac{f^2 - fx + x^2 + fx}{x}$ $D = \frac{f^2 + x^2}{x}$

Evaluating the Options:

• A. For distance between concave and convex $x = \frac{f}{2}$, then $D = \frac{5}{2}f$ Substitute $x = \frac{f}{2}$ into the derived formula for $D$: $D = \frac{f^2 + (\frac{f}{2})^2}{\frac{f}{2}} = \frac{f^2 + \frac{f^2}{4}}{\frac{f}{2}} = \frac{\frac{5f^2}{4}}{\frac{f}{2}} = \frac{5f^2}{4} \times \frac{2}{f} = \frac{5f}{2}$. This statement is correct.

• B. For $x = \frac{f}{2}$; virtual image is being formed by concave lens. For $x = \frac{f}{2}$, we calculated $v_c = \frac{f(f-\frac{f}{2})}{\frac{f}{2}} = \frac{f(\frac{f}{2})}{\frac{f}{2}} = f$. Since $v_c = +f$ (positive), the image formed by the concave lens is a real image (formed to the right of the concave lens by actual intersection of rays). This statement is incorrect.

• C. For $x = f$ the deviation caused by concave lens is zero. If $x = f$, the image $I_1$ formed by Lens 1 is at a distance $f$ from Lens 1. Since the concave lens is also at a distance $x=f$ from Lens 1, the image $I_1$ is formed exactly at the position of the concave lens. This means the rays from Lens 1 are converging towards the optical center of the concave lens. When rays pass through the optical center of any lens, they go undeviated. Therefore, the deviation caused by the concave lens is zero. This statement is correct. (Also, substituting $x=f$ into the formula for $D$: $D = \frac{f^2+f^2}{f} = \frac{2f^2}{f} = 2f$. This means the system acts like an afocal system, which is consistent with the rays passing undeviated through the middle lens.)

Since both A and C are correct, and the question asks for the correct option(s), we list both.