Question

For hydrogen like species, which of the following graphs provides the most appropriate representation of E vs Z plot for a constant n ? [E : Energy of the stationary state, Z : atomic number, n = principal quantum number] [2025]

Answer 1

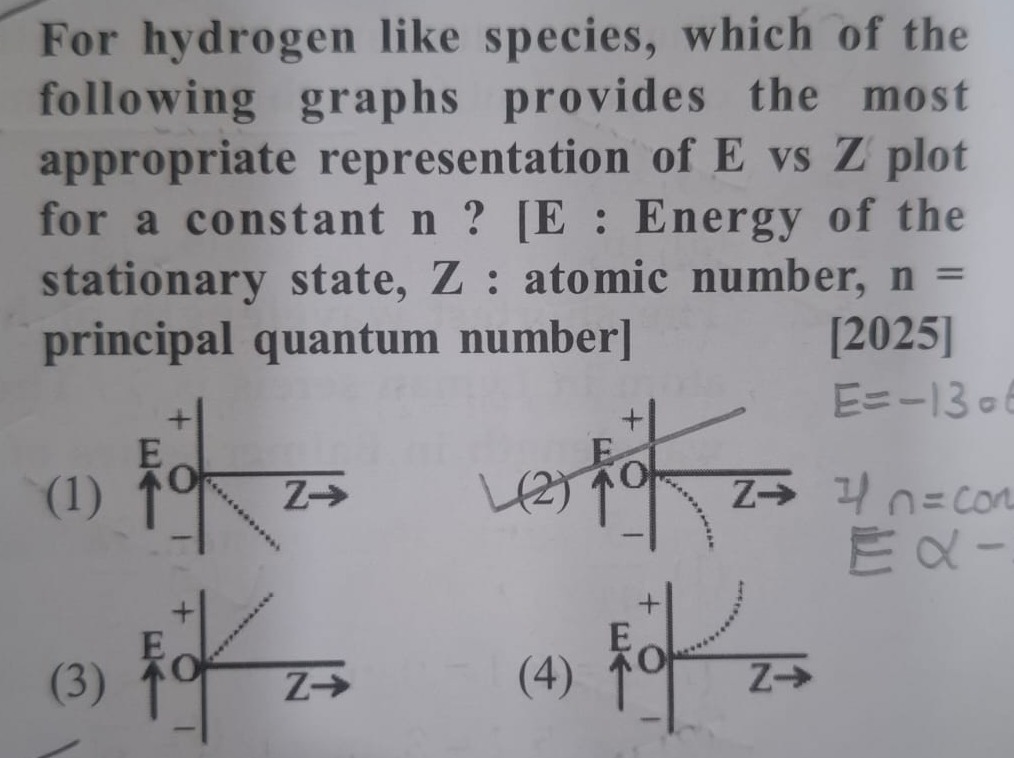
4

Answer 2

The energy of a stationary state for a hydrogen-like species is given by the Bohr model formula:

$E = -13.6 \frac{Z^2}{n^2} \text{ eV}$

where:

• $E$ is the energy of the stationary state.
• $Z$ is the atomic number.
• $n$ is the principal quantum number.

The problem states that $n$ is constant. Let's denote the constant value $\frac{-13.6}{n^2}$ as $C$. Since $n$ is a positive integer, $n^2$ is positive, and thus $C$ will be a negative constant. So, the relationship between $E$ and $Z$ can be written as:

$E = C \cdot Z^2$

where $C < 0$.

Let's analyze this relationship:

1. Nature of E: Since $C$ is negative and $Z^2$ is always positive (as $Z \ge 1$), the energy $E$ will always be negative. This means the graph should be in the region where E is below the Z-axis.
2. Dependence on Z: The energy $E$ is proportional to $Z^2$. This indicates a parabolic relationship.
3. Behavior as Z increases: As $Z$ increases, $Z^2$ increases. Since $C$ is negative, the value of $E$ will become more negative (i.e., its magnitude will increase, but the actual value will decrease).

Now let's examine the given graphs:

• The Z-axis (horizontal axis) represents the atomic number, which is always positive ($Z \ge 1$).

• The E-axis (vertical axis) represents energy. Positive E values are above the Z-axis, and negative E values are below the Z-axis.

• Graph (1): Shows a linear decrease in E with increasing Z, and E is negative. This is incorrect because the relationship is quadratic ($Z^2$), not linear.

• Graph (2): Shows a linear increase in E with increasing Z, and E is positive. This is incorrect because E should be negative and the relationship is quadratic. The dotted line shows a parabolic curve in the positive E region, which is also incorrect.

• Graph (3): Shows a linear increase in E with increasing Z, and E is positive. This is incorrect because E should be negative and the relationship is quadratic.

• Graph (4): Shows E values in the negative region (below the Z-axis). As Z increases, the curve goes further down, meaning E becomes more negative. The shape of the curve is a downward-opening parabola, which is consistent with $E = C \cdot Z^2$ where $C$ is a negative constant. This graph correctly represents the quadratic dependence and the negative nature of the energy for hydrogen-like species.

Therefore, Graph (4) provides the most appropriate representation.

Explanation of the solution: The energy of a hydrogen-like species is given by $E = -13.6 \frac{Z^2}{n^2}$. For constant $n$, $E$ is proportional to $-Z^2$. This means $E$ is always negative and its magnitude increases quadratically with $Z$. Graph (4) correctly depicts a downward-opening parabolic curve in the negative energy region as $Z$ increases.