Question

For He ion, the only incorrect combination is:

Column $1$	Column $2$	Column $3$
$1s$ Orbital	(i)$\;{\psi _{n,l,{m_l}}}\;a{\left( {\dfrac{Z}{{{a_0}}}} \right)^{\dfrac{3}{2}}}{e^{ - \left( {\dfrac{{{Z_r}}}{{{a_0}}}} \right)}}$	(P)
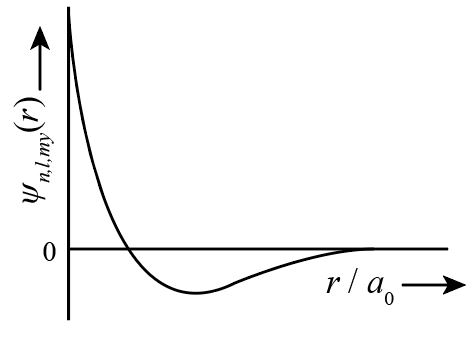$2s$ Orbital	(ii) one radial node	(Q) Probability density at nucleus
$2{p_z}$ Orbital	(iii) ${\psi _{n,l,{m_l}}}\;a{\left( {\dfrac{Z}{{{a_0}}}} \right)^{\dfrac{5}{2}}}r{e^{ - \left( {\dfrac{{{Z_r}}}{{{a_0}}}} \right)}}\cos \theta$	(R) Probability density is maximum at nucleus
$3d_z^2$ Orbital	(iv) xy-plane is a nodal plane	(S) Energy needed to excite an electron from $n = 2$ state to $n = 4$ state is $\dfrac{{27}}{{32}}$ times the energy needed to excite an electron from $n = 2$ state to $n = 6$ state.

A. (I) (iii) (R)
B. (II) (ii) (Q)
C. (I) (i) (S)
D. (I) (i) (R)

Answer 1

Helium ion is nothing but the one electron is given away form one s-orbital out of two and positive charge is acquired as we know that one electron is present in hydrogen is the same way only one electron will remain in the helium ion, hence it will behave as atom with only one electron.

Complete Step by step answer: As we know that hydrogen is the simplest atom containing only one electron. ${\rm{n,}}\,{\rm{l,}}\,{{\rm{m}}_{\rm{l}}}$ resembles the principle quantum number, azimuthal quantum number and magnetic quantum number respectively. Radial node is measured from ${\rm{n,}}\,{\rm{l}}$ values. The probability density of finding the electron is never $100\%$ because electrons are having Heisenberg uncertainty principle.
We will see the column one by one
In column 1, we will determine the radial nodes of the given orbitals by the formula
${\rm{radial}}\,{\rm{node = }}\,{\rm{n - l - 1}}$
For ${\rm{1s}}$orbital
$\Rightarrow {\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,1{\rm{ - 0 - 1 = }}\,0$
For ${\rm{2s}}$orbital
$\Rightarrow {\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,2{\rm{ - 0 - 1 = }}\,1$
For ${\rm{3}}{{\rm{p}}_z}$orbital
$\Rightarrow {\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,{\rm{3 - 1 - 1 = }}\,{\rm{1}}$
For ${\rm{3d}}_z^2$orbital
$\Rightarrow {\rm{radial}}\,{\rm{node}}\,{\rm{ = }}\,3{\rm{ - 2 - 1 = }}\,0$
Now, we could see from above explanation, the radial nodes is one for ${\rm{2s}}$ and ${\rm{3}}{{\rm{p}}_z}$ orbitals but the graph for ${\rm{2s}}$orbital is shown as
By the formula

{{\rm{R}}_{{\rm{2,0}}}}{\rm{ = }}\dfrac{{\rm{1}}}{{\sqrt {{\rm{32\pi }}} }}\dfrac{{\rm{1}}}{{{\rm{a}}_{\rm{0}}^{\dfrac{{\rm{3}}}{{\rm{2}}}}}}\left( {{\rm{2 - }}\dfrac{{\rm{r}}}{{{{\rm{a}}_{\rm{0}}}}}} \right){{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{\rm{r}}}{{{\rm{2}}{{\rm{a}}_{\rm{0}}}}}} \right)}\\\ {\rm{y = }}\left( {{\rm{2 - x}}} \right)\,{{\rm{e}}^{{\rm{ - x}}}} \end{array}$$ Appling above formula we have values along $${\rm{x}}$$and $${\rm{y}}$$ direction as-  And the graph for $${\rm{3}}{{\rm{p}}_z}$$orbital is shown as-  **Therefore, our correct option is option (A) (I) (iii) (R).** **Note:** $${{\rm{\varphi }}_{{\rm{n,l,}}{{\rm{m}}_{\rm{l}}}}}{\rm{a}}{\left( {\dfrac{{\rm{Z}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)^{\dfrac{{\rm{3}}}{{\rm{2}}}}}{{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)}$$ belongs to orbital $${\rm{1s}}$$ where principle quantum number can be calculated by $${{\rm{e}}^{\rm{ - }}}^{\left( {\dfrac{{{\rm{Zr}}}}{{{{\rm{a}}_{\rm{0}}}}}} \right)}$$ and azimuthal quantum number is calculated by minimum power of $${\rm{r}}$$ or maximum power of $${\rm{Sin\theta Cos\theta }}$$. Energy of one-dimensional box is calculated by – $${{\rm{E}}_{\rm{x}}}{\rm{ = }}\dfrac{{{\rm{n}}_{\rm{x}}^{\rm{2}}{{\rm{h}}^{\rm{2}}}}}{{{\rm{8m}}{{\rm{l}}^{\rm{2}}}}}$$ Helium ion is nothing but the one electron is given away form one s-orbital out of two and positive charge is acquired as we know that one electron is present in hydrogen is the same way only one electron will remain in the helium ion, hence it will behave as atom with only one electron.