Question

For given circuit, charges on capacitor ${{C}_{1}}\text{ and }{{\text{C}}_{2}}$ in steady state will be equal to:

& \text{A) }{{\text{C}}_{1}}|{{V}_{A}}-{{V}_{C}}|,{{C}_{2}} |{{V}_{C}}-{{V}_{B}}|\text{ respectively} \\\ & \text{B) }{{\text{C}}_{1}}|{{V}_{A}}-{{V}_{B}}|, {{C}_{2}}|{{V}_{A}}-{{V}_{B}}|\text{ respectively} \\\ & \text{C) (}{{\text{C}}_{1}}+{{C}_{2}})|{{V}_{A}}-{{V}_{B}}|\text{ on each capacitor} \\\ & \text{D) }\left( \dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}} \right)|{{V}_{A}}-{{V}_{B}}|\text{ on each capacitor} \\\ \end{aligned}$$

Answer 1

The charge accumulated on a capacitor is directly proportional to the capacitance C and voltage across the capacitance V. We are given the different values of potential at each end which has a net effect on each capacitance in the whole network.

Complete step-by-step solution:
We know that the capacitance of a capacitor is the ability of a pair of parallel plates to store the electrical charges on the plates at a given voltage. The capacitance is related to the charge accumulated on the plates and the voltage as –
$C=\dfrac{Q}{V}$
The charge accumulated on a parallel plate capacitor is, therefore, given as –
$Q=CV$
Now, let us consider the situation given to us in which the capacitors ${{C}_{1}}\text{ and }{{\text{C}}_{2}}$ are connected to external sources ${{\text{V}}_{\text{A}}}\text{,}{{\text{V}}_{\text{B }}}\text{and }{{\text{V}}_{\text{C}}}$ through the resistor R as shown in the circuit given below.

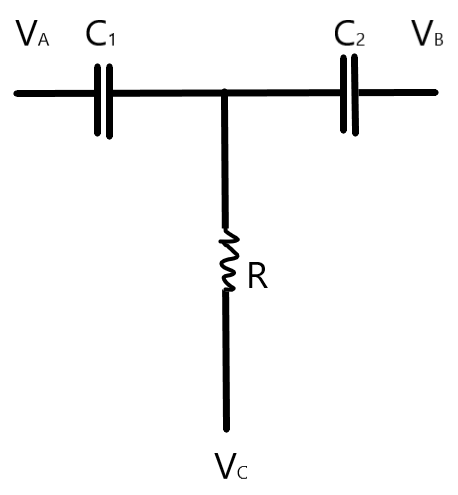
Now, we understand that in the given circuit the node joining the capacitors has a potential which is equal to the ${{\text{V}}_{C}}$.
So, we can understand that the potential across the capacitors ${{C}_{1}}\text{ and }{{\text{C}}_{2}}$ can be given as –
Across the capacitor ${{C}_{1}}$, the voltage is –
${{V}_{1}}={{V}_{A}}-{{V}_{C}}$
Across the capacitor ${{C}_{2}}$, the voltage is –
${{V}_{2}}={{V}_{B}}-{{V}_{C}}$
Now, we can find the charge in each of the capacitor by using the relation between the voltage and the capacitance of the capacitor as explained earlier –
$Q=CV$
For the capacitor ${{C}_{1}}$, the charge accumulated is given as –

& {{Q}_{1}}={{C}_{1}}{{V}_{1}} \\\ & \therefore {{Q}_{1}}={{C}_{1}}({{V}_{A}}-{{V}_{C}}) \\\ \end{aligned}$$ For the capacitor $${{C}_{2}}$$, the charge accumulated is given as – $$\begin{aligned} & {{Q}_{2}}={{C}_{2}}{{V}_{2}} \\\ & \therefore {{Q}_{2}}={{C}_{2}}({{V}_{B}}-{{V}_{C}}) \\\ \end{aligned}$$ So, we get the charge accumulated on both the capacitors. **The correct answer is option A.** **Note:** The resistance used in the circuit avoids the shorting of the circuit in case the capacitors reach a breakdown. The electric field developing inside the capacitor can exceed the ionizing energy of the electric field in the air resulting in conduction without resistance.