Question

For gaseous state, if most probable speed is denoted by ${C^*}$, average speed by $\overline C$ and root mean square speed by C, then for large number of molecules the ratio of these speeds are:
a- ${C^*}$: $\overline C$ : C = 1.128 : 1.225 : 1
b- ${C^*}$: $\overline C$ : C = 1 : 1.128 : 1.225
c- ${C^*}$: $\overline C$ : C = 1 :1.125 : 1.128
d- ${C^*}$: $\overline C$ : C = 1.125 : 1.128 : 1

Answer 1

The given three representations of velocity are related to each other by following formula:
${C^*}$: $\overline C$ : C = $\sqrt {\dfrac{{2RT}}{M}}$ : $\sqrt {\dfrac{{8RT}}{{\pi M}}}$: $\sqrt {\dfrac{{3RT}}{M}}$

Complete answer:
Kinetic Molecular Theory explains the macroscopic properties of gases and can be used to calculate the different kinds of gaseous speeds. Measuring the velocities of particles at a given time results in a large distribution of values; some particles may move very slowly, others very quickly, and because they are constantly moving in different directions, the velocity could equal zero.
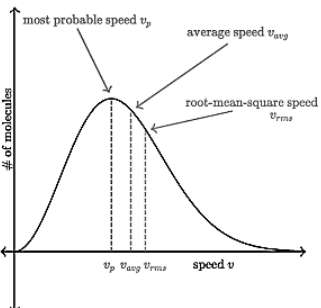
-Most probable speed (${C^*}$): The most probable speed is the speed most likely to be possessed by any molecule of the same mass m in the gaseous system and corresponds to the maximum value. And it is given by the following formula:
C*= $\sqrt {\dfrac{{2RT}}{M}}$
-Average speed ($\overline C$): Movement of gaseous molecules is in random speeds and in random directions. The Maxwell-Boltzmann Distribution describes the average speeds of collection gaseous particles at a given temperature. And it is given by:
$\overline C$=$\sqrt {\dfrac{{8RT}}{{\pi M}}}$
-Root mean square speed (C or ${C_{rms}}$): As the name represents roots of mean of squares of the velocities is known as the root-mean-square (RMS) velocity, and it is represented as follows:
C or ${C_{rms}}$=$\sqrt {\dfrac{{3RT}}{M}}$
On comparing these three velocities:
${C^*}$: $\overline C$ : C = $\sqrt {\dfrac{{2RT}}{M}}$ : $\sqrt {\dfrac{{8RT}}{{\pi M}}}$: $\sqrt {\dfrac{{3RT}}{M}}$
=$\sqrt 2 :\sqrt {\dfrac{8}{\pi }} :\sqrt 3$
=1 : 1.128 : 1.225

So, the correct option is (B) 1: 1.128: 1.225 .

Note:
Most probable speed, average speed, and root mean square speed are related to each other by the formula stated above.Their relation can be expressed as a graph as shown below: