Question

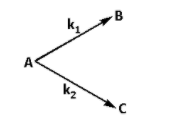
For first order parallel reaction ${{\text{k}}_1}$ and ${{\text{k}}_2}$ are ${\text{4}}$ and $2{\text{ mi}}{{\text{n}}^{ - 1}}$ respectively at $300{\text{ K}}$. If the activation energies for the formation of B and C are respectively ${\text{30,000}}$ and $38,314{\text{ joule/mol}}$ respectively.
The temperature at which B and C will be obtained in equimolar ratio is:

(A) $757.48{\text{ K}}$
(B) $378.74{\text{ K}}$
(C) $600{\text{ K}}$
(D) None of these

Answer 1

The minimum amount of energy that the reacting species must possess to undergo a specific reaction is known as the activation energy. The relation between the temperature, rate constant and activation energy is given by the Arrhenius equation.

Complete step by step solution:
We know the expression for the relationship between the rate constant of a first order reaction and the activation energy is as follows:
$k = A \times {e^{\left( { - \dfrac{{{E_a}}}{{R \times T}}} \right)}}$
Where $k$ is the rate constant of a first order reaction,
$A$ is the pre-exponential factor,
${E_a}$ is the energy of activation,
$R$ is the universal gas constant,
$T$ is the temperature.
Thus,
${k_1} = {A_1} \times {e^{\left( { - \dfrac{{{E_{a1}}}}{{R \times T}}} \right)}}$ …… (1)
And,
${k_2} = {A_2} \times {e^{\left( { - \dfrac{{{E_{a2}}}}{{R \times T}}} \right)}}$ …… (2)
Thus,
$\dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{A_1}}}{{{A_2}}} \times {e^{\dfrac{{\left( {{E_{a2}} - {E_{a1}}} \right)}}{{R \times T}}}}$
We are given that ${{\text{k}}_1}$ and ${{\text{k}}_2}$ are ${\text{4}}$ and $2{\text{ mi}}{{\text{n}}^{ - 1}}$ respectively, the energies of activation are ${\text{30,000}}$ and $38,314{\text{ joule/mol}}$ respectively. Substitute $8.314{\text{ J }}{{\text{K}}^{ - 1}}{\text{ mo}}{{\text{l}}^{ - 1}}$ for the universal gas constant, $300{\text{ K}}$ for the temperature. Thus,
$\dfrac{4}{2} = \dfrac{{{A_1}}}{{{A_2}}} \times {e^{\dfrac{{\left( {38314 - 30000} \right)}}{{8.314 \times 300}}}}$
Taking log on both the sides of the equation, we get,
$\log 2 = \log \left( {\dfrac{{{A_1}}}{{{A_2}}}} \right) + \dfrac{{8314}}{{8.314 \times 2.303 \times 300}}$
$\Rightarrow \log \left( {\dfrac{{{A_1}}}{{{A_2}}}} \right) = \log 2 - 1.4473$
$\Rightarrow \log \left( {\dfrac{{{A_1}}}{{{A_2}}}} \right) = \log 2 - 1.4473$
$\Rightarrow \log \left( {\dfrac{{{A_1}}}{{{A_2}}}} \right) = 0.3010 - 1.4473$
$\Rightarrow \log \left( {\dfrac{{{A_1}}}{{{A_2}}}} \right) = - 1.1463$
We are given an equimolar ratio. For an equimolar ratio,
${k_1} = {k_2}$ …… (3)
Substitute equation (1) and equation (2) in equation (3). Thus,
${A_1} \times {e^{\left( { - \dfrac{{{E_{a1}}}}{{R \times T}}} \right)}} = {A_2} \times {e^{\left( { - \dfrac{{{E_{a2}}}}{{R \times T}}} \right)}}$
$\Rightarrow \dfrac{{{A_1}}}{{{A_2}}} = {e^{\left( { - \dfrac{{{E_{a2}} - {E_{a1}}}}{{R \times T}}} \right)}}$
Taking log on both the sides of the equation, we get,
$\log \dfrac{{{A_1}}}{{{A_2}}} = - \dfrac{{{E_{a2}} - {E_{a1}}}}{{2.303 \times R \times T}}$
We are given that the energies of activation are ${\text{30,000}}$ and $38,314{\text{ joule/mol}}$ respectively. Substitute $8.314{\text{ J }}{{\text{K}}^{ - 1}}{\text{ mo}}{{\text{l}}^{ - 1}}$ for the universal gas constant. Thus,
$- 1.1463 = - \dfrac{{\left( {38314 - 30000} \right){\text{ J mo}}{{\text{l}}^{ - 1}}}}{{2.303 \times 8.314{\text{ J }}{{\text{K}}^{ - 1}}{\text{ mo}}{{\text{l}}^{ - 1}} \times T}}$
$\Rightarrow T = - \dfrac{{{\text{8314}}}}{{2.303 \times 8.314 \times - 1.1463}}$
$\Rightarrow T = 378.74{\text{ K}}$
Thus, the temperature at which B and C will be obtained in equimolar ratio is $378.74{\text{ K}}$.

Thus, the correct option is (B) $378.74{\text{ K}}$.

Note: The reactions in which a substance decomposes or reacts in one or more ways are known as parallel reactions. The parallel reactions are also known as side reactions. The reaction that depends on the concentration of one reactant only is known as the first order reaction.