Question

For every twice differentiable function, $f:R\to \left[ -2,2 \right]$ with ${{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}=85$, which of the following statement (s) is/are true?
A. There exists $r,s\in R$ where $rB. There exits${{x}{0}}\in \left( -4,0 \right)$such that$\left| f'\left( {{x}{0}} \right) \right|\le 1$. C.$\underset{x\to \alpha }{\mathop{\lim }},f\left( x \right)=1$. D. There exists$\alpha \in \left( -4,4 \right)$such that$f\left( \alpha \right)+f'\left( \alpha \right)=0$and$f'\left( \alpha \right)\ne 0$.

Answer 1

We will apply the definition of one-one. In a one-one function, we have that every element of the domain must have (only) exactly one pre-image. That is for $f\left( a \right)=f\left( b \right)$ we have a =b, where a and b are points in the domain. We will apply the mean value theorem. Let $f$ be continuous on [a, b] and differentiable on (a, b), then there exists a constant $c\in \left( a,b \right)$ such that $f'\left( c \right)=\dfrac{f\left( b \right)-f\left( a \right)}{b-a}$.

Complete step-by-step answer :
We are given with a type of function whose domain is all real numbers and range lies between [-2, 2] and equation ${{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}=85$. Now we will consider the cases one by one.
In the first statement, we have to check the property of a function which says that $f\left( x \right)$ is a one to one function. For a function to have a property like this, it must satisfy the definition of one-one. It states that the corresponding element of every pre image or range must belong to only one, meaning exactly one, corresponding element of the domain. Let us consider the following graphs.

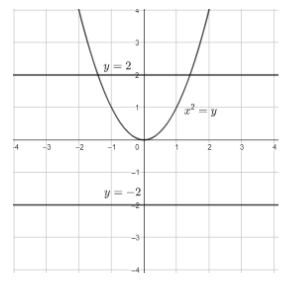
This graph is not one-one because its elements in range do not have their exact corresponding pre-images in domain. Now we will consider the following graph.

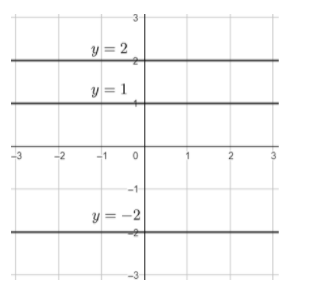
This graph is also not one-one because the graph is constant here. In this constant function, the elements of range have the same pre-images in domain. According to the question, if there exists any graph that lies between range [-2, 2] then it will make the first statement true. For example: $y={{x}^{3}}$ as shown below is one-one within the range [-2, 2].

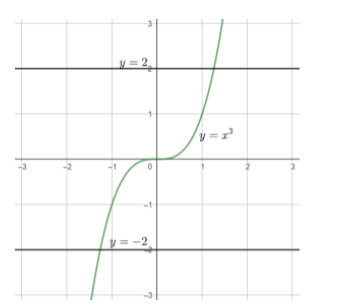
Hence, we answer, taking the above graphs as a guideline that the graph cannot be constant here. Therefore, the function is one-one. Hence option A is the right option.
Now we will consider the second statement. We will apply the mean value theorem here. In this theorem, we have a function that is continuous on [a, b] and differentiable on (a, b). Then there exists $c\in \left( a,b \right)$ such that we have $f'\left( c \right)=\dfrac{f\left( b \right)-f\left( a \right)}{b-a}$. By the statement B, we have ${{x}_{0}}\in \left( -4,0 \right)$ such that $\left| f'\left( {{x}_{0}} \right) \right|\le 1$. Therefore, we can write, $\left| f'\left( {{x}_{0}} \right) \right|=\left| \dfrac{f\left( 0 \right)-f\left( -4 \right)}{0-4} \right|$. If we notice $\left| f'\left( {{x}_{0}} \right) \right|\le 1$ clearly, then we need to find a number for which $\left| \dfrac{f\left( 0 \right)-f\left( -4 \right)}{0-4} \right|$ is less than or equal to 1. Since, we are not given any function, we will consider that by the interval [-2, 2], that results in a minimum value of -2 and maximum value of 2. For the function $\left| \dfrac{f\left( 0 \right)-f\left( -4 \right)}{0-4} \right|$ to have a maximum value, it needs to have $f\left( 0 \right)$ as maximum and $f\left( -4 \right)$ as minimum function values. Since -2 is minimum and 2 is maximum in codomain or range. Therefore, we have $\left| f\left( 0 \right)-f\left( -4 \right) \right|\le 2-\left( -2 \right)$ which is 4. Thus, we get,
$\begin{aligned} & \left| f'\left( {{x}_{0}} \right) \right|\le \left| \dfrac{4}{-4} \right| \\\ & \Rightarrow \left| f'\left( {{x}_{0}} \right) \right|\le \left| -1 \right| \\\ & \Rightarrow \left| f'\left( {{x}_{0}} \right) \right|\le 1 \\\ \end{aligned}$
Hence, option B is the right option.
Now, we will consider the third option, $\underset{x\to \alpha }{\mathop{\lim }}\,f\left( x \right)=1$. To verify this statement, we will consider a function $f\left( x \right)$ which is given by ${{x}^{2}}+\sqrt{15}x+\sqrt{70}$ . By differentiating it by the formula $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$. Therefore, we can write $f'\left( x \right)=\sqrt{15}+2x$. By substituting x = 0, we get,$f\left( 0 \right)=\sqrt{15}\left( 0 \right)+\sqrt{70}\Rightarrow f\left( 0 \right)=\sqrt{70}\Rightarrow f'\left( 0 \right)=\sqrt{15}$. Now we will consider the function’s condition as ${{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}=85$. We will consider the left hand side of the function, so,
$\begin{aligned} & {{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}={{\left( \sqrt{70} \right)}^{2}}+{{\left( \sqrt{15} \right)}^{2}} \\\ & \Rightarrow {{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}=70+15 \\\ & {{\left( f\left( 0 \right) \right)}^{2}}+{{\left( f'\left( 0 \right) \right)}^{2}}=85 \\\ \end{aligned}$
But the limit of $f\left( x \right)$ is not equal to 1. Hence, option C is not the right option.
Now we will consider option D. Let us say we are given a function $f\left( x \right)=0x$, where $x\in \left( -4,4 \right)$ such that $x=0,f\left( 0 \right)+f'\left( 0 \right)=0$. As $f\left( 0 \right)=2\left( 0 \right)=0$ and $f\left( x \right)=0\Rightarrow f'\left( x \right)=0$. So, by substituting in $f\left( 0 \right)+f'\left( 0 \right)=0+0$. We need to check if $f'\left( 0 \right)=0$or not. Clearly $f\left( x \right)=0$, so $f'\left( 0 \right)=0$. Therefore, option D is wrong.
Hence, the correct options are option A and B.

Note : In option A verification, since there are no functions mentioned, we have to consider two different functions with one-one condition as well as not one-one condition. By this we will find the answer of the one-one condition. By considering option C, we can take a function $f\left( x \right)=\sin \left( \sqrt{85}x \right)$. This will also result in option C as wrong. In option D verification, we took a default function. Alternatively, we can choose any other function satisfying the condition $f\left( \alpha \right)+f'\left( \alpha \right)=0$ for $\alpha \in \left( -4,4 \right)$, but $f'\left( \alpha \right)=0$. This will also result in option D as the wrong option.