Question

For ensuring dissipation of the same energy in all three resistors $({R_1},{R_2},{R_3})$ connected as shown in the figure, their values must be related as

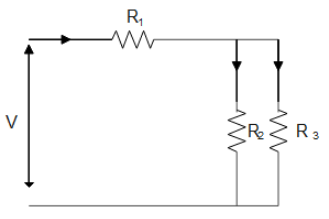
A. ${R_1} = {R_2} - {R_3}$
B. ${R_2} = {R_3}{\text{ and }}{R_1} = 4{R_3}$
C. ${R_2} = {R_3}{\text{ and }}{R_1} = \dfrac{{{R_2}}}{4}$
D. ${R_1} = {R_2} + {R_3}$

Answer 1

We need to find the values of the three resistors arranged as shown in the figure such that the energy dissipated in the three resistors is equal. We need to use the concepts of parallel and series connection of the resistors and also apply Kirchhoff’s current law to get the required values.

Complete step by step answer:
We will draw the circuit diagram and label the current through the different resistors. We know that the current through the series connection of the resistors is the same for each resistor. And for parallel connection, the current is different through the different resistors and thus we have three currents flowing through the three resistors as shown in the figure.

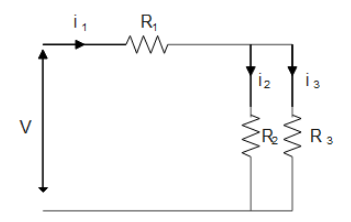
According to Kirchhoff’s current law, the current through the first resistor will be equal to the summation of the current through the other two resistors. Hence we get
${i_1} = {i_2} + {i_3} - - - (1)$
Now using Ohm’s law we get the power or energy dissipated across each resistor which is the same as in the question is given by
${i_1}^2{R_1} = {i_2}^2{R_2} = {i_3}^2{R_3} - - - \left( 2 \right)$
Now since the second and third resistors are in parallel connection, therefore, the voltage drop across the resistors will be the same hence we get
${i_2}{R_2} = {i_3}{R_3} - - - \left( 3 \right)$
Dividing equation $2$ with the equation $3$ we get
${i_2} = {i_3} \Rightarrow {R_2} = {R_3}$
Hence using the results in the equation $1$ we get
${i_1} = 2{i_2}$
Putting the value in the equation $2$ we get
${i_1}^2{R_1} = \dfrac{{{i_1}^2}}{4}{R_2} \\\ \therefore {R_1} = \dfrac{1}{4}{R_2}$

Hence option C is the right answer.

Note: Note that according to Kirchhoff’s current law the current entering a junction or a node is equal to the current leaving the junction or node and hence the current flowing the resistor will be equal to the sum of the currents through the other two resistors.