Question
Question: For different values of resistance, \[R\] power consumption in \[R\] are given. Then which of the fo...
For different values of resistance, R power consumption in R are given. Then which of the following values are not possible?
(A) 2W
(B) 5W
(C) 8W
(D) 4W
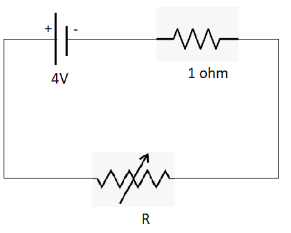
Solution
First of all, we will find the net current in the circuit. After that we will find the power in the resistor R . To find the maximum power, we will equate the first order derivative of power to zero. Then we can find the maximum power for the found-out value of resistance.
Complete step by step answer:
In the given question, we are supplied with the following data:
There is a cell in the circuit whose potential difference is 4 volts along with a fixed resistor and a variable resistor.
The value of the fixed resistor is one ohm and the variable resistor is represented by R .
To begin with, we know that the value of the resistance can be changed with the help of a variable resistor. More is the value of resistance in the circuit, higher is the power consumption.The power in the circuit is minimum when the resistance in the variable resistor is zero ohms. However, we don’t know the value of the resistance at which the power consumed in the circuit is maximum. We will try to find this out.
Power in the circuit is given by:
P=i2R …… (1)
Where,
P indicates the power consumed in the circuit.
i indicates total current in the circuit.
R indicates the resistance.
We have, the net resistance in the circuit is (R+1) ohms.
From Ohm’s law, the current in the circuit is given as:
i=R+1V
Since, potential difference is 4 volts, so we have:
i=R+14
Now, we use the expression of current in equation (1) and we get:
P = {i^2}R \\\
\Rightarrow P = {\left( {\dfrac{4}{{R + 1}}} \right)^2} \times R \\\
\Rightarrow P = \dfrac{{16}}{{{{\left( {R + 1} \right)}^2}}} \times R \\\
We know that for the maximum value of a quantity, the value first order derivative is always zero.
Mathematically, we can write:
\dfrac{{dP}}{{dR}} = 0 \\\
\Rightarrow \dfrac{d}{{dR}}\left[ {\dfrac{{16}}{{{{\left( {R + 1} \right)}^2}}} \times R} \right] = 0 \\\
\Rightarrow \dfrac{d}{{dR}}\left[ {16{{\left( {R + 1} \right)}^{ - 2}} \times R} \right] = 0 \\\
We apply chain rule for derivative here:
16R\left( { - 2} \right){\left( {R + 1} \right)^{ - 3}} + 16{\left( {R + 1} \right)^{ - 2}} = 0 \\\
\Rightarrow \dfrac{{ - 32R}}{{{{\left( {R + 1} \right)}^3}}} + \dfrac{{16}}{{{{\left( {R + 1} \right)}^2}}} = 0 \\\
\Rightarrow \dfrac{{ - 32R + 16R + 16}}{{{{\left( {R + 1} \right)}^3}}} = 0 \\\
\Rightarrow - 16R + 16 = 0 \\\
\Rightarrow 16R = 16 \\\
\Rightarrow R = \dfrac{{16}}{{16}} \\\
\Rightarrow R = 1\,\Omega \\\
Therefore, the power in the circuit is maximum for resistance 1Ω in the resistor R .
So, the maximum power is found out as:
P=(R+1)216×R ⇒P=(1+1)216×1 ⇒P=2216 ∴P=4W
Hence, the maximum power in the circuit can be 4W and it cannot be either 5W or 8W .
The correct option is D.
Note: While solving this problem, many students seem to have confusion regarding the power. Remember that the power is minimum when the value of resistance in the variable resistor is zero. However, to find out the maximum power condition, we must equate the first order derivative of power to zero. After we find the limit of power, we then exclude the values present above the limit.
