Solveeit Logo
Login

Question

Question: For complex numbers, \[{{z}_{1}},{{z}_{2}}\]if \[\left| {{z}_{1}} \right|=12\]and \[\left| {{z}_{2}}...

For complex numbers, z1,z2{{z}_{1}},{{z}_{2}}if ∣z1∣=12\left| {{z}_{1}} \right|=12and ∣z2−3−4i∣=5\left| {{z}_{2}}-3-4i \right|=5 then minimum value of ∣z1−z2∣\left| {{z}_{1}}-{{z}_{2}} \right| is
1. 00
2. 22
3. 77
4. 1717

Explanation

Solution

To get the solution of the given question you can use two different approaches. First one is to draw the figure of the given expression and then find out the minimum value of ∣z1−z2∣\left| {{z}_{1}}-{{z}_{2}} \right|. Or else you can use the property of complex numbers i.e. mod of difference of the complex numbers.

Complete step by step answer:
To solve this question we can use two different approaches. One is by using the diagram and the other is by using the properties of complex numbers.
Let us discuss both the approaches one by one.
By making the diagrams of the given data we are able to find the minimum value of ∣z1−z2∣\left| {{z}_{1}}-{{z}_{2}} \right|.
It is given that ∣z1∣=12\left| {{z}_{1}} \right|=12, this expression means that there is a circle of radius 1212and the center points are (0,0)(0,0)
And the second expression is ∣z2−3−4i∣=5\left| {{z}_{2}}-3-4i \right|=5,
If we simplify this expression, we get
∣z2−(3+4i)∣=5\left| {{z}_{2}}-(3+4i) \right|=5
By this expression we can say that there is a circle of radius 55 with the center points at (3,4)(3,4)
By having the knowledge of this data, we can represent both the expression as

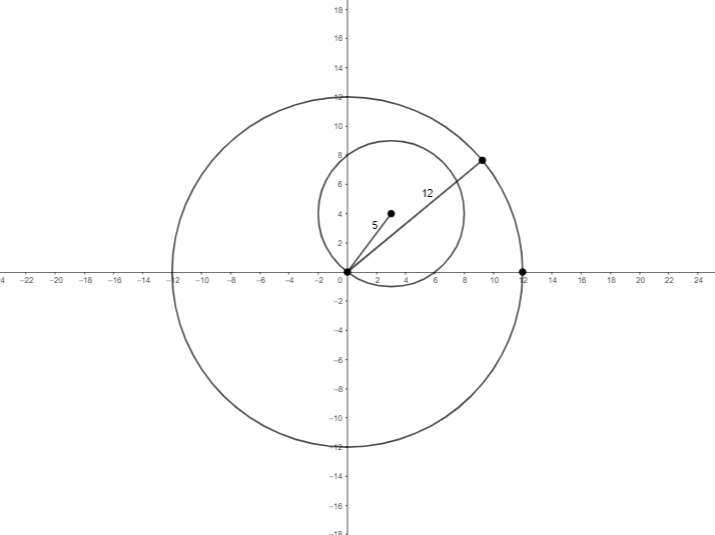
If the radius of the expression ∣z2−(3+4i)∣=5\left| {{z}_{2}}-(3+4i) \right|=5is 55then we can easily find the diameter of the circle by multiplying radius by 22. So the diameter of the circle is 1010.
From the figure we can clearly say,

& \Rightarrow \min \left| {{z}_{1}}-{{z}_{2}} \right|=12-10 \\\ & \Rightarrow \min \left| {{z}_{1}}-{{z}_{2}} \right|=2 \\\ \end{aligned}$$ Hence, we can say that $$2$$is the final answer. **So, the correct answer is “Option 2”.** **Note:** Complex numbers are the numbers that can be represented in the form of $$a+ib$$, where $$a$$ is the real part of the complex number and $$b$$is the imaginary part of the complex numbers. $$0$$is both a real number as well as a complex number because $$0$$can be represented as $$0+0i$$this implies that $$0$$is also a complex number. Now using the second approach i.e. properties of the complex numbers, We know that for two complex numbers $${{z}_{1}}$$ and $${{z}_{2}}$$, $$\left| {{z}_{1}}-{{z}_{2}} \right|\ge \left| {{z}_{1}} \right|-\left| {{z}_{2}} \right|$$ Apply this property in the L.H.S of the expression, $$\left| {{z}_{2}}-(3+4i) \right|=5$$ We can calculate the magnitude by rooting the terms of summation of squares of real part and imaginary part. $$\left| {{z}_{2}}-(3+4i) \right|\ge \left| {{z}_{2}} \right|-\left| 3+4i \right|$$ $$\left| {{z}_{2}}-(3+4i) \right|\ge \left| {{z}_{2}} \right|-\sqrt{{{3}^{2}}+{{4}^{2}}}$$ $$\Rightarrow \left| {{z}_{2}} \right|\ge 10$$ We are required to find the minimum value of $$\left| {{z}_{1}}-{{z}_{2}} \right|$$. Again applying the same property, we get $$\left| {{z}_{1}}-{{z}_{2}} \right|\ge \left| {{z}_{1}} \right|-\left| {{z}_{2}} \right|$$ Now putting the values, we get $$\Rightarrow \left| {{z}_{1}}-{{z}_{2}} \right|\ge 12-10$$ $$\Rightarrow \left| {{z}_{1}}-{{z}_{2}} \right|\ge 2$$ The value for $$\left| {{z}_{1}}-{{z}_{2}} \right|$$ is equal to or greater than $$2$$. But we have to find the minimum value. Hence $$2$$is the minimum possible value.