Question

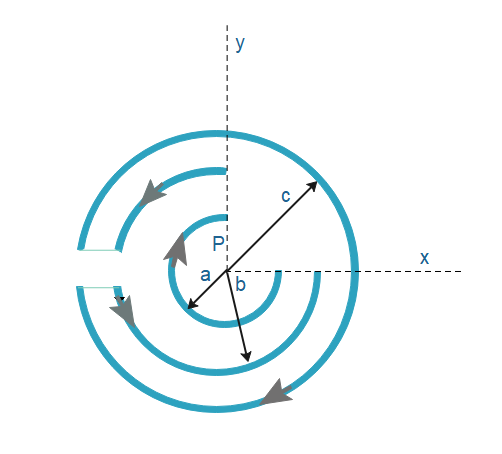
For $c=2a$ if, the magnetic field at point P will be zero when
$\begin{aligned} & \text{A}\text{. }a=b \\\ & \text{B}\text{. }a=\dfrac{3}{5}b \\\ & \text{C}\text{. }a=\dfrac{5}{3}b \\\ & \text{D}\text{. }a=\dfrac{1}{3}b \\\ \end{aligned}$

Answer 1

The direction of the magnetic field depends on the direction of the current flowing through the coil or loop. The direction of the magnetic field is given by right-hand rule. Since the magnetic field is a vector quantity, for calculating the resultant magnetic field you need to consider direction also. If magnetic fields have opposite directions then resultant will be the difference of those two and if they have the same direction then resultant will be the sum of those two.

Formula used:
$B=\dfrac{{{\mu }_{0}}I}{2a}\left( \dfrac{\theta }{\pi } \right)$
Where,
$B=\text{ magnetic field}$
$I=\text{ Current flows in conductor}$
$a=\text{Radius}$
$\theta =\text{Angle traced by circle}$

Complete step by step answer:
Before solving this question, we need to understand some rules and symbols for the representation of the magnetic field.
If the direction of the current is counterclockwise then the direction of the magnetic field $B$ is inside the page.
If the direction of the current is clockwise then the direction of the magnetic field $B$ is out of the page.
Here we need to find out a condition or relation between $a,b\text{ and c}$ such that the magnetic field at point $P$ must be zero.
First, let’s find the magnetic field of each circle i.e. $a,b\text{ and c}$
The magnetic field of the circle of radius $a$ is given by,
$\begin{aligned} & {{B}_{a}}=\dfrac{{{\mu }_{0}}I}{2a}\left( \dfrac{3\pi }{4\pi } \right) \\\ & {{B}_{a}}=\dfrac{{{\mu }_{0}}I}{2a}\dfrac{3}{4} \\\ \end{aligned}$
Here the direction of the magnetic field is inside the page.
Magnetic field of circle of radius $b$ is given by,
$\begin{aligned} & {{B}_{b}}=\dfrac{{{\mu }_{0}}I}{2a}\left( \dfrac{3\pi }{4\pi } \right) \\\ & {{B}_{b}}=\dfrac{{{\mu }_{0}}I}{2b}\dfrac{3}{4} \\\ \end{aligned}$
Here the direction of the magnetic field is out of the page.
The magnetic field of the circle of radius $c$ is given by,
$\begin{aligned} & {{B}_{c}}=\dfrac{{{\mu }_{0}}I}{2a} \\\ & \because c=2a \\\ & {{B}_{c}}=\dfrac{{{\mu }_{0}}I}{4a} \\\ \end{aligned}$
Here the direction of the magnetic field is inside the page.
Consider, the sign will be positive for the direction of the magnetic field inside the page and the sign will be negative for the direction of the magnetic field out of the page.
Therefore,

& {{B}_{a}}+{{B}_{c}}={{B}_{b}} \\\ & \dfrac{{{\mu }_{0}}I}{2a}\dfrac{3}{4}+\dfrac{{{\mu }_{0}}I}{4a}=\dfrac{{{\mu }_{0}}I}{2b}\dfrac{3}{4} \\\ \end{aligned}$$ $\begin{aligned} & \left( \dfrac{3}{2}+1 \right)\dfrac{1}{a}=\dfrac{3}{2}b \\\ & a=\dfrac{5}{3}b \\\ \end{aligned}$ **Answer - $(C)$** **Note:** The direction of the magnetic is always perpendicular to the direction of the current flow and the plane of the coil. If you curl your finger along the coil and the direction in which your fingers are wrapped give the direction of current flow then the thumb pointing outwards gives the direction of the magnetic field. If you consider the coil is placed in the plane of paper then the magnetic field is perpendicular to the plane of the paper and directed inwards if the current flows in a clockwise direction and directed outwards if current flows in an anticlockwise direction.