Question
Question: For Balmer series, wavelength of first line is \('{\lambda _1}'\) and for Brackett series, wavelengt...
For Balmer series, wavelength of first line is ′λ1′ and for Brackett series, wavelength of first line is ′λ2′then λ2λ1 is
A) 0.081
B) 0.162
C) 0.198
D) 0.238
Solution
Hint
The wavelength for the transition from one orbit to other is given by λ1=R(n121−n221). First find the wavelength for the first line of the Balmer series from n=3 to n=2. Similarly the wavelength of the first line of Brackett series from n=5 to n=4 is calculated. Now divide the first wavelength by the second to get the ratio.
Complete step by step answer
When the electron is transition from one energy level to another that is to is given by,
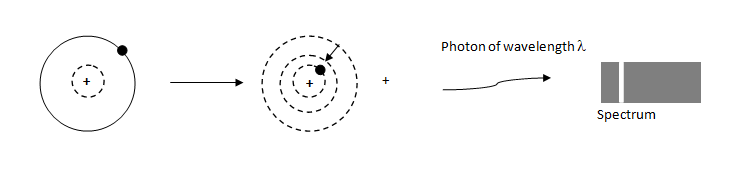
λ1=R(n121−n221)
For first line of Balmer series from n=3 to n=2,
λ11=R(221−321)
λ1=R7.2
For first line of Brackett series,
λ21=R(421−521)
λ2=R44.44
The ratio of λ2λ1 ,
λ2λ1=R7.2×44.44R
λ2λ1=0.162
Hence, the ratio equal to 0.162 and the correct option is (B)
Note
When an electron makes transition from higher energy level to a lower energy level then a photon of frequency υis emitted.
Energy of the emitted radiation is given by,
ΔE=13.6Z2(n121−n221)
Frequency of the emitted radiation is given by,
υ=RcZ2(n121−n221)
Recoiling of an atom is given by,
Recoil=hRZ2(n121−n221)
