Question
Question: For any two sets \(S\) and \(T\), \(S\Delta T\) is defined as the set of all elements that belong to...
For any two sets S and T, SΔT is defined as the set of all elements that belong to either S or T but not both, that is SΔT=(S∪T)−(S∩T). Let A, B and C be sets such that A∩B∩C=ϕ, and the number of elements in each of AΔB, BΔC and CΔA equals to 100. Then the number of elements in A∪B∪C equals
Solution
We will use the formula, n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C) to find the value of number of elements ofA∪B∪C. We will then substitute the value of A∩B∩C=ϕ. We will then use the Venn diagram to find the value of the unknowns.
Complete step-by-step answer:
We have to find the value of A∪B∪C
We know that n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
Also, we are given that A∩B∩C=ϕ and n(A∩B∩C)=0
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A) eqn. (1)
We are also given that
n(AΔB)=100 ⇒n((A∪B)−(A∩B))=100
Let us now simplify the expression (A∪B)−(A∩B) using Venn-Diagram.
If A and B are two sets, then the intersection includes only the common portion and the union includes all the elements of both the sets.
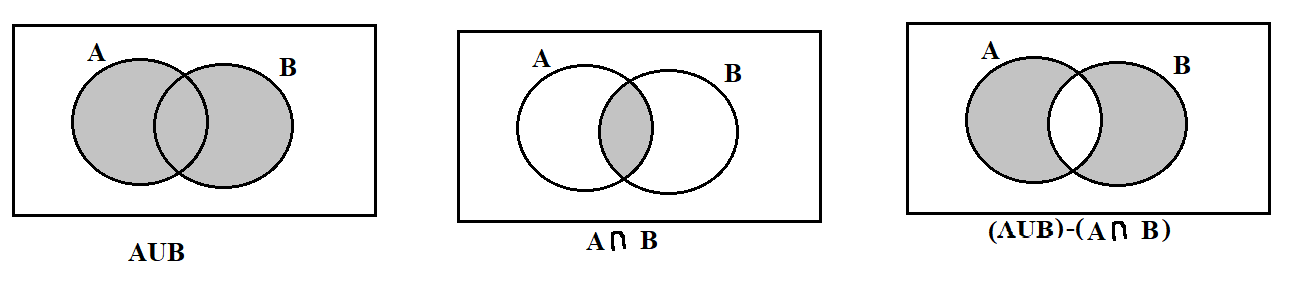
Hence, n((A∪B)−(A∩B))=n(A)+n(B)−n(A∩B)
Similarly, we can write this for any two sets.
Therefore, we can write equation (1) as
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A) ⇒n(A∪B∪C)=(n(A)+n(B)−n(A∩B))+n(C)−n(B∩C)−n(C∩A)
Here, we do not have any condition on the number of intersections of two sets, therefore, A∪B∪C cannot be determined.
Note: We use Venn diagrams to represent the sets. A∪B is the set of elements from both the sets A and B, similarly, A∩B has all common elements of A and B. The set A−B has the elements of set A which are not a part of A∩B.
