Question

For any two sets prove that: $A-\left( A\cap B \right)=A-B$

Answer 1

Hint:We will draw the Venn diagram to prove the above statement. We will also state some definitions to make the understanding part more clear and after that we will take some values of A, U and B to show that $A-\left( A\cap B \right)=A-B$ is true.

Complete step-by-step answer:
Let’s first draw the required Venn diagram for LHS.
First we will draw $A\cap B$

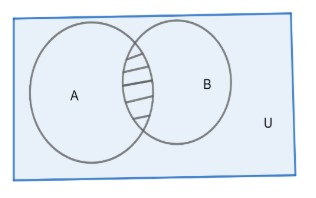
Now we will draw Venn diagram of $A-\left( A\cap B \right)$ is,

Now we will draw the Venn diagram of RHS, A – B

From these diagrams also we can see that LHS = RHS.
Union: The union (denoted by $\cup$ ) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
Intersection: The intersection of two sets has only the elements common to both sets. If an element is in just one set it is not part of the intersection. The symbol is an upside down $\cap$ .
When we subtract two sets the common elements of the set which is being subtract is removed.
Like in this case the region A – B will be $A$ - $A\cap B$ because the shaded region is the common region that lies in both A and B, hence when we subtract B from A we have to remove the common elements between them from A, and the common element or region is $A\cap B$ the shaded region.
Hence, we have proved $A-\left( A\cap B \right)=A-B$.
Now let’s take some value of A,U and B.
Let,
A = { 1, 2, 3 }
B = { 3, 4 }
U = { 1, 2, 3, 4, 5 }
Now A = { 1, 2, 3 } and B = { 3, 4 }, the common element is 3.
Therefore,
$A\cap B$ = { 3 }
Now, A = { 1, 2, 3 } and $A\cap B$ = { 3 } the common element is 3, so we have to remove that from set A.
After removing we get,
$A$ - $A\cap B$= { 1, 2 }
Now A = { 1, 2, 3 } and B = { 3, 4 }, the common element is 3, so we have to remove that from set A.
After removing we get,
$A – B$ = { 1, 2 }
Hence, we can see that $A-\left( A\cap B \right)=A-B$ is true.

Note: The definition of all the terms that we have used should be kept in mind. One can take some other values of A, B and U and can check the relation $A-\left( A\cap B \right)=A-B$, just to be more sure and get a better idea.